Projeto de Laboratório - Cálculo 1

2º semestre de 2003

Prof.: Célius A. Magalhães

Autores:

Felipe Gonçalves Labanca - 03/77627

Vitor Fernandes Ribeiro de Oliveira -03/90631

Lívia Andréia Gomes -03/82841

Clarissa Lima Chagas -03/74997

Construindo um Silo

Projeto de Laboratório - Cálculo 1

Objetivo: Determinar as dimensões de um silo para que, considerando qualquer volume, seu custo seja mínimo.

Introdução: Enfim férias. Para podermos gozar do nosso precioso descanso após um longo semestre de estudos, nosso grupo de recém aprovados em cálculo 1 decide ir a um hotel-fazenda. Após alguns dias de estadia, reparamos que uma construção estava sendo realizada perto à produção de milho da fazenda. Curiosos, fomos descobrir o que era. Após conversarmos com o dono do local (um fazendeiro muito agradável, porém com certa dificuldade com números), ele nos apresentou o projeto. Um silo, desenhado pelo próprio fazendeiro, que decidira comprar o material com o dinheiro reservado para a obra e usar seus funcionários para montá-lo. Percebemos, porém, que o dinheiro a ser gasto estava muito alto para a obra, e decidimos dar uma mãozinha.

O Problema: Um silo será construído (exceto a base) na forma de um cilindro sob um hemisfério. O custo da construção por unidade de área da superfície é duas vezes maior para o hemisfério em relação ao lado do cilindro. Determinar as dimensões para um volume fixo com custos de produção minimizados. Ignore a espessura das paredes e o desperdício durante a construção.

Iniciando...

[> restart;
[>

Preliminares:

Começaremos atribuindo variáveis ao problema. Consideraremos ' r ' como o raio do hemisfério (que coincide com o raio da base do cilindro), ' h ' como a altura do cilindro, ' V ' como o volume total do silo e, por ser considerado como um valor fixo, ' v0' como sendo um valor do volume qualquer para o silo.

É interessante também lembrar as fórmulas volume do cilindro = Pi*r^2*h , area do cilindro = 2*Pi*r*h , volume da esfera = (4/3)*Pi*r^3 e area da esfera = 4*Pi*r^2.

Mãos à obra:

Primeiro devemos definir o volume. Para isso, definiremos primeiro o volume do cilindro (V1) e o volume do hemisfério (V2), e a seguir, definiremos V como sendo a soma dos dois volumes. Nota: volume do hemisferio = (volume da esfera)/2 . [>V1:=Pi*r^2*h; V2:=((4/3)*Pi*r^3)/2; V:=V1+V2;

[>

Aproveitando os cálculos, definiremos a área da superfície. Analogamente aos cálculos anteriores, A1 será a área do cilindro, A2 a área do hemisfério e A=A1+A2. Não confunda! area do hemisferio = (area da esfera)/2 .
[> A1:=2*Pi*r*h; A2:=(4*Pi*r^2)/2; A:=A1+A2;

[>

Está melhorando! Agora podemos ver qual o custo do material a ser utilizado. Definiremos por C tal custo. Para defini-lo, decidimos indicar o preço como sendo proporcional às unidades de área medidas. Podemos assim, atribuir o custo da parte cilíndrica do silo como sendo a própria função de sua área. Portanto, C1 (custo da área cilíndrica) será 2*Pi*r*h. Porém, por ser o dobro do preço para ser feita a parte do hemisfério, definiremos o C2 (custo da área esférica) como sendo 2 vezes a sua área (. Armazenando os dados obtidos, temos:
[> C1:=2*Pi*r*h; C2:=2*(4*Pi*r^2)/2; C:=C1+C2;

[>

Resolvendo: após definirmos todas as expressões que nos serão úteis, convém adaptá-las para podermos explorá-las ainda mais. Começaremos usando a expressão do volume para deixar a altura ( h ) em função do raio ( r ). Para tanto, utilizaremos a expressão do volume, isolando o ' h ' - usaremos a função isolate do maple para isso. Vale lembrar que o volume ( v0 ) é independente e, portanto, usado como um valor constante, que substituirá o valor V dependente do r e do h .
[> isolate(V=v0,h);

[>

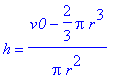
[> h0:=(v0-2/3*Pi*r^3)/Pi/r^2;

[>

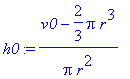
Para deixarmos o custo ( C ) em função de apenas uma variável, substituiremos o valor da altura encontrado. Assim, teremos o custo em função apenas do raio. Definiremos assim a função C(r) :
[> C:=r->2/r*(v0-2/3*Pi*r^3)+4*Pi*r^2;

[>

Está ficando muuuuito interessante... Agora temos o custo em função do raio. Para podermos usufruir da poderosa arma dos máximos e mínimos do cálculo, devemos derivar a função C(r), e definir como dC(r) tal derivada. Vamos lá:
[> Diff(C(r),r)=diff(C(r),r);

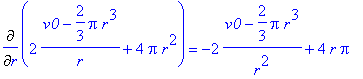
[> dC:=unapply(diff(C(r),r),r): 'dC(r)'=dC(r);

[>

Oba!!!! Agora, com a derivada podemos calcular os pontos críticos da função C(r). resolvendo a equação dC(r)=0, podemos achá-los. Vamos tentar:
[>solve(dC(r)=0,r);

[>

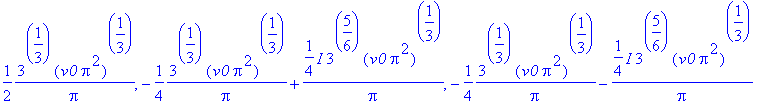
Definindo o raio como sendo única raíz real obtida acima, temos:
[>r:=1/2/Pi*3^(1/3)*(v0*Pi^2)^(1/3);

[>

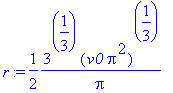
Usando o comando simplify do Maple, podemos simplificar sua definição e torná-la mais agradável. Assim:
[> simplify(r);

[>

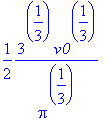
Yupiiiii!!! Achamos o raio que minimiza os custos da construção. Pronto... agora só falta encontrar a melhor altura do cilindro e pronto. E basta solicitarmos o valor de h0 para acharmos a altura, pois por estar em função de r , e o raio ter sido definido, a expressão é automaticamente calculada. Usaremos o comando simplify para adequá-lo ainda mais.
[> simplify(h0);

[>

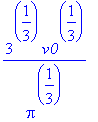
Resposta: Após concluir todos os nossos cálculos, informamos ao bondoso fazendeiro os valores do raio (da base do cilindro e, portanto, do hemisfério) e a altura do cilindro, ambos citados abaixo.
[>'r'=simplify(r);
   'h0'=simplify(h0);

[>

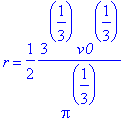
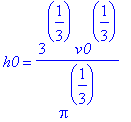
Com tais dados, o próximo passo é analisar com o fazendeiro a quantidade da produção do milho, e com a taxa de escoamento (saída do milho), determinar o volume necessário de armazenamento e, com tal volume, substituir o v0 na equação da altura e do raio.