Viu como você viu!

1.ª Atividade Tutorial de Cálculo - Uma Variável

Objetivo : justificar o estudo do comportamento de funções por meio de exemplos de modelagem de situações simples, enfatizando a relação entre o modelo e o problema em estudo; introduzir algumas funções predefinidas e ilustrar a definição de outras; introduzir alguns comandos básicos, ilustrando como usá-los no estudo do modelo proposto

Introdução

Se você está se perguntando por que estudar Cálculo, parabéns, é uma pergunta oportuna. O Cálculo pode ser usado no estudo de uma variedade surpreendente de situações, desde o movimento de planetas, passando por aparelhos eletroeletrônicos, até problemas de controle de qualidade do meio-ambiente. O que há de comum a essas situações é a possibilidade de modelá-las por meio da linguagem de funções e, em uma primeira resposta, este é talvez o principal objetivo do Cálculo: o estudo do comportamento de funções.

Aqui, procura-se ilustrar como um problema pode ser modelado usando a linguagem das funções, e de como essa linguagem pode ser útil a uma melhor compreensão da situação em estudo.

Preliminares

A principal diferença entre o Maple e um editor de textos é que, além dessas linhas, ditas linhas de texto, há também as linhas de comando, que são precedidas do sinal [>, como as duas linhas exemplificadas abaixo. É nessas linhas que as operações matemáticas podem ser solicitadas, o que deve ser feito por meio de comandos específicos. Para que um comando seja executado, basta posicionar o cursor sobre ele e pressionar a tecla "Enter". Como exemplo, execute o próximo comando, que indica como a operação de soma deve ser solicitada. Observe que a resposta é dada no centro da página, na cor azul.
[> 2+2;

Observe ainda o sinal de ponto e vírgula no final do comando, sem o qual ele não será executado. Verifique que esse sinal é mesmo indispensável procurando executar o próximo comando, que indica como a multiplicação deve ser solicitada.
[ > 2*2

Warning, premature end of input

Viu! Assim, nada de esquecer esse sinal em seus comandos. Para que produza a resposta esperada, volte ao comando acima e acrescente o ponto e vírgula, reexecutando-o em seguida.

Uma linha de comando pode ser introduzida em qualquer lugar do texto. Para isso, basta posicionar o cursor no lugar onde se quer introduzir a linha e, em seguida, pressionar o botão [> da barra de ferramentas no topo da tela. Experimente essa opção introduzindo uma linha de comando no espaço em branco a seguir. De fato, é fortemente recomendado que essas linhas sejam introduzidas aos pares, como feito acima. Isso porque, após a execução de um comando, o cursor salta para a próxima linha de comando e, não havendo uma dessas linhas imediatamente abaixo, o cursor pode saltar para um lugar incerto e não sabido, a algumas dezenas de linhas daqui. Em seguida, aproveite a oportunidade e solicite a divisão de oito por dois executando o comando 8/2 (faça isso na linha de comando, claro, e ... não se esqueça do ponto e vírgula!).
[ > 8/2;

Pronto. Isso é o bastante para por mãos à obra.

O Problema

Uma empresa que aluga painéis publicitários, conhecidos como "outdoors", instalou um deles em frente a uma calçada com um bom fluxo de pessoas. O painel, com 5,98 m de largura e 3,70 m de altura, foi instalado com sua base a 3 m do piso, para dificultar a ação dos pichadores.

Tendo em vista que, quanto mais perto, mais fácil seria ver o painel, os operários que fizeram a instalação escolheram o lugar mais próximo possível da calçada. No entanto, o painel ficou tão próximo que os passantes tinham que fazer um grande esforço para vê-lo. A empresa percebeu o erro e, após um estudo matemático da situação, indicado abaixo, obteve a "melhor distância" em que o painel deveria ser instalado para que o ângulo de visão fosse o "melhor possível". O painel foi então mudado de posição e, tanto para comemorar como para chamar a atenção dos anunciantes, a empresa escreveu no painel os dizeres "Viu como você viu!".

Primeiras Observações

A situação está ilustrada na figura abaixo, em que v representa o ângulo de visão do observador, em radianos, e OP representa, em metros, a distância do observador ao painel. Considerou-se que o olho do observador, a uma altura de 1.7 m do solo, está na posição O, e daí a distância de 1.3 m indicada na figura, pois a base do painel encontra-se a 3.0 m do solo.

O problema consiste, então, em determinar a distância OP, representada por x, de modo que o ângulo v seja o maior possível , e para isso é necessário determinar como esse ângulo depende da variável x.

Nesse sentido, observe que, de acordo com a Figura 1, o triângulo OPQ é retângulo, e os comprimentos dos catetos OP e PQ são iguais a x e 1.3, respectivamente. Os quadrados desses comprimentos podem ser calculados por meio do acento circunflexo ^ , como indica o comando a seguir. Como visto acima, para executá-lo basta posicionar o cursor sobre o comando e pressionar a tecla "Enter".
[> 1.3^2; x^2;

Indicando por h0 o comprimento da hipotenusa OQ do triângulo OPQ, pelo teorema de Pitágoras seque-se que
[> h0=sqrt(1.3^2+x^2);

Observe como a raiz quadrada deve ser solicitada, por meio do comando sqrt (abreviação de square root ). A igualdade h0 = sqrt(1.3^2 + x^2) será usada várias vezes, e é conveniente definir h0 como sendo igual a sqrt(1.3^2 + x^2). Isso pode ser feito por meio do sinal de definição := , composto do sinal de dois pontos : e do sinal de igual = , mas sem espaço entre eles. Usando esse sinal, pode-se definir o valor de h0 com o comando
[> h0:=sqrt(1.3^2+x^2);

Este comando foi obtido da seguinte maneira: primeiro, usando o mouse , selecionou-se o comando anterior; em seguida, aquele comando foi copiado usando o botão "copiar" da barra de ferramentas; depois, o cursor foi posicionando na linha de comando acima e pressionando o botão "colar" ; finalmente, o sinal de definição foi introduzido no novo comando. Esse recurso, de copiar e colar, é importante por evitar erros de digitação. Após essa definição, o símbolo h0 passa a ser equivalente a sqrt(1.3^2 + x^2), e será substituído por essa expressão nos comandos envolvendo esse símbolo. Por exemplo, como resposta à solicitação do valor de h0, obtém-se, como esperado,
[> h0;

A definição de h0 pode ser usada para calcular tanto o seno como o coseno do ângulo u. De fato, da Figura 1 segue-se que sen(u) = 1.3 / h0 (cateto oposto dividido pela hipotenusa). Analogamente, cos(u) = x / h0 (cateto adjacente dividido pela hipotenusa). Assim, o seno e o coseno de u são dados, respectivamente, por
[> 1.3/h0; x/h0;

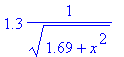
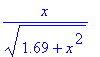
Exercícios

1) Voltando a consultar a Figura 1, observe que o triângulo OPR também é retângulo. Copie então o comando que define h0 e, em seguida, adapte-o para definir como h1 o comprimento da hipotenusa OR do triângulo OPR.
[> h1:=sqrt(5^2+x^2);

2) Copie o comando acima que calcula o seno e o coseno de u. Em seguida, adapte-o para calcular o seno e o coseno do ângulo t.
[> 5/h1; x/h1;

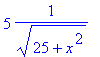
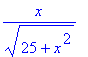
3) Como verificação do exercício anterior, some o quadrado do seno com o quadrado do coseno e verifique se o resultado é igual a 1, como deve. Verifique atentamente o resultado porque, provavelmente, o Maple não fará todas as simplificações possíveis.
[> (5/h1)^2+(x/h1)^2;

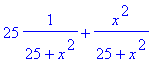
Dois Comandos Interessantes

Após as definições acima, é natural perguntar sobre os valores de h0 e h1 para valores dados de x. Por exemplo, qual é o valor de h0 para x = 3? Em uma primeira tentativa, pode-se substituir manualmente x = 3 na expressão de h0 = sqrt(1.3^2 + x^2), e obter o valor
[> sqrt(1.3^2+3^2);

No entanto, em casos mais elaborados, isso pode ser trabalhoso. Uma outra forma, mais elegante, é usar o comando subs , como ilustrado a seguir.
[> subs(x=3,h0);

Observe que o comando subs deve ser usado a partir de duas informações, ditas entradas do comando. Na primeira entrada deve-se informar qual a substituição a ser feita e, na segunda, em qual expressão a substituição deve ser implementada.

Outro comando, tão interessante quanto o subs , e o comando solve , usado para resolver equações. Por exemplo, qual deve ser o valor de x para que o ângulo u, ilustrado na Figura 1, seja igual a / 6? Ora, o seno de / 6 é igual a 0.5 e o seno de u é igual a 1.3 / h0. Logo, basta resolver a equação 1.3 / h0 = 0.5 na variável x, onde h0 = sqrt(1.3^2 + x^2) já foi definido anteriormente. Para resolver esta equação, usa-se o comando solve como ilustrado abaixo. Novamente, este comando possui duas entradas: a primeira é a equação a ser resolvida e, a segunda, a variável em que se deve resolver a equação.
[> solve(1.3/h0=0.5,x);

Caramba! Essa brincadeira está ficando interessante. Mas vale a pena verificar o resultado. Para isso, pode-se substituir o valor de x = 2.25166050 na expressão 1.3 / h0 e verificar se o resultado é igual a 0.5. E, de fato, tem-se
[> subs(x=2.251666050,1.3/h0);

Perfeito! Os comandos estão funcionando como deviam, e já se tem confiança nos resultados obtidos.

Nos exercícios a seguir, será necessário voltar a consultar a Figura 1 do início da seção "Primeiras Observações". Para isso existe o " B ookmark", uma ferramenta que permite navegar por toda a atividade. Para usá-la, clique no menu " V iew" da barra de ferramentas no topo da tela e, em seguida, selecione a opção " B ookmark". Após esse procedimento, deve aparecer um índice de todas as seções e exercícios da atividade. Clique então em "Primeiras Observações" para ir ao início daquela seção. Em seguida, para voltar a esse ponto, repita o procedimento escolhendo, dessa vez, o "Exercício 4".

Exercícios

4) Substitua x = 3 na expressão 5 / h1 para calcular o sen(t) nesse caso. Observe que, agora, o resultado não está na forma decimal como antes, mas vá adiante!
[> subs(x=3,5/h1);

5) A forma decimal é conhecida também como a de "ponto flutuante" ( floating-point ). Para obter a expressão decimal do resultado do exercício anterior, pode-se usar o comando evalf(subs(x=3,5/h1)) ("eval" de evaluar e "f" de floating-point ). Execute então esse comando (na linha de comando, claro!), e observe que o resultado é maior que 0.8.
[> evalf(subs(x=3,5/h1));

6) O coseno do ângulo t é igual a x / h1 e o coseno de / 6 é igual a sqrt(3) / 2. Usando essas informações e o comando solve , determine o valor de x para o qual o ângulo t é igual a / 6. Use ainda o evalf para verificar que o resultado e superior a 8.5.
[> evalf(solve(x/h1=sqrt(3)/2,x));

7) As definições de h0 e h1 facilitaram muito os cálculos acima. Mas agora é necessário saber o que deve ser feito para que h0 e h1 voltem a ser o que sempre foram, isto é, valores genéricos. Para isso, a maneira mais educada é usar novamente o sinal de definição, mas desta vez em conjunto com as aspas simples. Por exemplo, para que h0 volte a ser um valor genérico, usa-se o comando h0:='h0' . Digite então esse comando (na linha de comando!). Em seguida, solicite os valores de h0 e h1, como foi feito anteriormente, e verifique que a resposta apenas repete o símbolo h0, mas mantém a definição de h1.
[> h0:='h0'; h0; h1;

8) Uma outra maneira, um tanto truculenta, é usar o comando restart (reiniciar). Esse comando faz com que todas as definições sejam ignoradas, voltando-se à estaca zero. Apesar de truculento, esse comando será usado com freqüência para descartar definições que deixaram de ser necessárias. Execute então esse comando e, em seguida, solicite os valores de h0 e h1. Observe que, agora, a resposta a esses comandos apenas repete os símbolos h0 e h1.
[> restart; h0; h1;

O Ângulo de Visão

"Muito bem. Até aqui está tudo muito engraçadinho. Mas, lamentavelmente, nada ainda foi dito sobre o que é importante: o ângulo v com que o observador vê o painel! Afinal, qual a razão de todos esses cálculos?"

É verdade, essa é uma crítica séria. Mas os ângulos t e u são importantes para o estudo do ângulo v. Isso porque, consultando mais uma vez a Figura 1 (olha o " B ookmark"...), obtém-se que v = t - u. Assim, sen(v) = sen(t - u), e sabe-se que sen(t - u) pode ser expresso em termos de sen(u), cos(u), sen(t) e cos(t) por meio de uma identidade trigonométrica. Essa identidade é "conhecida" pelo Maple, e pode ser obtida usando-se o comando expand , como indicado abaixo.

Antes, é necessário dizer que as funções seno e coseno já estão predefinidas no Maple, sendo indicadas por sin e cos , respectivamente (abreviações de sine e cosine ). Compare então as respostas ao ser solicitado apenas sin(t - u) e ao ser solicitada essa mesma expressão precedida do expand .
[> sin(t-u); expand(sin(t-u));

Para ser usada logo a seguir, define-se essa identidade como sendo eq1 , uma abreviação para "equação 1".
[> eq1:=expand(sin(t-u));

Ótimo! Não poderia ser melhor, pois as expressões de sin(u), sin(t), cos(u) e cos(t) são conhecidas em função de x, e basta substituir essas expressões na eq1 . Para isso, lembre-se que as hipotenusas h0 e h1 são dadas por
[> h0:=sqrt(1.3^2+x^2); h1:=sqrt(5^2+x^2);

Logo, para substituir sin(u) = 1.3 / h0 na eq1 , basta usar o comando (adivinha o que significa eq2 !)
[> eq2:=subs(sin(u)=1.3/h0,eq1);

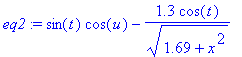
Exercícios

9) Procedendo de maneira análoga (o que significa copiar, colar e adaptar!), substitua cos(u) = x / h0 na eq2 , e defina o resultado como sendo eq3 . O resultado deve ser uma expressão que depende apenas de x, sin(t) e cos(t).
[> eq3:=subs(cos(u)=x/h0,eq2);

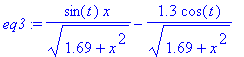
10) As duas substituições restantes podem ser feitas simultaneamente com um só comando. Para isso, na primeira entrada do subs , deve ser indicado o conjunto das substituições a serem feitas, isto é, o conjunto {sin(t) = 5 / h1, cos(t) = x / h1}, cujos elementos estão entre chaves e separados por vírgula. Copie então o comando que define a eq3 e mude o nome para eq4 . Em seguida, na primeira entrada do comando subs , inclua o conjunto das substituições a serem feitas. Finalmente, na segunda entrada, mude de eq2 para eq3 , para que a substituição seja implementada nessa última equação. Pronto, execute o comando e observe que o resultado apresenta a expressão 3.7*x no numerador e o produto de dois radicais no denominador.
[> eq4:=subs({sin(t)=5/h1,cos(t)=x/h1},eq3);

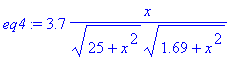
Reiniciando ...

Algumas definições acima serão usadas na próxima seção, mas nem todas... O comando a seguir tem o objetivo de selecionar apenas o que é essencial, evitando sobrecarregar a memória do computador com informações desnecessárias. Esse recurso será usado com freqüência nessas atividades. Sempre que for encontrado um " Reiniciando ... " não perca tempo: execute o comando que o segue.
[> restart; eq4:=3.7/(25+x^2)^(1/2)*x/(1.69+x^2)^(1/2);

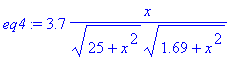
A Modelagem

A eq4 é o valor de sin(v) = sin(t - u) em função de x, isto é,
[> sin(v)=eq4;

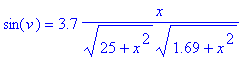
o que já é uma boa notícia. Outra boa notícia é que o ângulo v está sempre no intervalo [0, /2] e, nesse intervalo, o seno é uma função crescente. Assim, determinar o maior valor possível de v é equivalente a determinar o maior valor possível de sin(v). Este fato pode ser melhor compreendido a partir dos gráficos que serão apresentados no final da atividade. Até lá, e para dar continuidade ao raciocínio, admita este fato como verdadeiro.

Dessa forma, o problema fica reduzido a determinar o valor de x para o qual a eq4 assume o maior valor possível. Esse valor de x é a distância do painel à calçada que torna o ângulo de visão o maior possível.

O próximo passo é transformar a eq4 em uma função, de modo a facilitar o seu estudo. Acompanhe os passos abaixo com atenção, uma vez que definir funções será um dos procedimentos mais usados nessas atividades . Para isso, observe primeiro que a eq4 é o quociente entre duas funções, denotadas, por exemplo, por g(x) = 3.7*x e h(x) = sqrt(25 + x^2)*sqrt(1.69 + x^2) . Usando essa notação, a função g(x) pode ser definida com o comando
[> g:=x->3.7*x;

Esse exemplo ilustra a forma geral em que as funções são definidas: primeiro, o nome da função (g, h etc.) seguido do sinal de definição := ; depois, o nome da variável independente (no caso, a variável x) seguido do sinal -> , que é composto do traço de separação de sílabas - e do sinal de maior > ; finalmente, a expressão da função propriamente dita. Uma vez definida, tanto o valor genérico g(x) como os valores em pontos específicos, como g(1), g(2) etc., podem ser solicitados com os comandos
[> g(x); g(1); g(2);

Exercícios

11) Adivinhe que exercício é esse!! Definir a função h(x), claro! Para isso, copie a definição da função g(x) e faça as adaptações necessárias. Em seguida, para verificação, solicite o valor genérico de h(x) e alguns valores específicos que você achar interessantes (!?).
[> h:=x->sqrt(25+x^2)*sqrt(1.69+x^2); h(x); h(1); h(2);

12) As funções g(x) e h(x) podem agora ser manipuladas de forma natural, por exemplo, multiplicando-as g(x)* h(x) ou dividindo-as g(x) / h(x). Defina então como sendo f(x) o quociente dessas duas funções. Para isso, como g(x) e h(x) já foram definidas, basta executar o comando f:=x->g(x)/h(x) . Copie então esse comando para a linha de comando e acrescente o indispensável ponto e vírgula. Em seguida, solicite o valor genérico de f(x), e verifique que é exatamente a expressão da eq4 .
[> f:=x->g(x)/h(x); f(x);

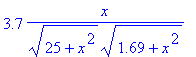
13) Pronto. Isso conclui a modelagem do problema, uma vez que a eq4 está agora na forma de uma função. Expressões como "a melhor distância" e "o melhor ângulo" foram quantificadas e tornadas precisas. O problema está agora reduzido a determinar o valor de x para o qual a função f(x) assume o valor máximo. Nesse sentido, do valor máximo, solicite o valor de f(x) para x = 1, 2, 3, 4 e 5, e observe que essa seqüência de valores é crescente no início e decrescente no final. Talvez seja necessário usar o evalf para facilitar a comparação entre os valores solicitados.
[> evalf(f(1)); evalf(f(2)); evalf(f(3)); evalf(f(4)); evalf(f(5));

Reiniciando ...

Mais uma vez, o comando a seguir seleciona apenas as definições que serão necessárias na próxima seção, e não deixe de executá-lo .
[> restart; f:=x->3.7/(25+x^2)^(1/2)*x/(1.69+x^2)^(1/2);

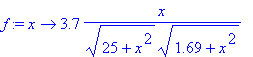
O Problema e o Modelo

Para ilustrar como o ângulo v depende da distância x, pode-se usar o recurso de "animação", como na figura abaixo. Esse recurso será melhor explorado posteriormente e, por enquanto, basta clicar sobre a figura e observar a nova barra de ferramentas no topo da tela, com comandos semelhantes aos de um gravador. Nessa nova barra, clique sobre o botão correspondente ao "play" para dar início à animação. Em seguida, procure determinar as funções dos demais botões dessa nova barra.

A largura da figura está própria para se perceber o comportamento do ângulo v para valores pequenos da distância x. Mas a largura pode ser alterada com o auxílio do mouse . Para isso, primeiro clique sobre a animação e observe os quadradinhos que aparecem em sua moldura; em seguida, posicione o ponteiro do mouse sobre um desses quadradinhos e observe que ele se transforma em uma seta dupla; nessa posição, e com o botão esquerdo do mouse pressionado, arraste a moldura de forma a aumentar a sua largura. Repita a animação após esse procedimento, e observe o comportamento do ângulo para distâncias maiores.

Após os procedimentos indicados acima, percebe-se a seguinte relação entre a distância x e o ângulo v: a partir de x = 0, em que v = 0, esse ângulo aumenta à medida que x aumenta, até alcançar um valor máximo, a partir do qual o ângulo passa a diminuir. Esse comportamento deve estar refletido na função f(x), uma vez que f(x) = sin(v). Espera-se, portanto, que f(x) seja uma função crescente para valores de x próximos de zero, e uma função decrescente para valores grandes de x. Esse comportamento de fato se verifica, como ilustram os próximos exercícios.

Exercícios

14) Verifique que, para x = 0, 0.5, 1, 1.5 e 2, os valores de f(x) são crescentes. Para isso, talvez seja necessário usar novamente o evalf .
[> evalf(f(0)); evalf(f(0.5)); evalf(f(1)); evalf(f(1.5)); evalf(f(2));

15) Analogamente (copiar, colar e adaptar!), verifique que, para x = 5, 10, 15, 20 e 25, os valores de f(x) são decrescentes.
[> evalf(f(5)); evalf(f(10)); evalf(f(15)); evalf(f(20)); evalf(f(25));

16) Os exercícios acima indicam que f(x) assume um valor máximo para algum x entre 2 e 5, em que o intervalo [2, 5] tem comprimento 5 - 2 = 3. Mas essa estimativa pode ser melhorada. Para isso, determine um intervalo de comprimento 1 e que ainda contenha o ponto x no qual a função f(x) assume um valor máximo. Calcule outros valores de f(x), se necessário, e justifique a sua resposta no espaço indicado abaixo.
[> evalf(f(1.5)); evalf(f(2)); evalf(f(2.5)); evalf(f(3)); evalf(f(3.5));

Resposta : a função f(x) deve assumir um valor máximo em algum ponto x entre os valores 2 e 3. Isso porque os valores de f(x) crescem para x menor que 2, e decrescem para x maior que 3. Além disso, f(2.5) é maior que f(2) e f(3).

17) O que foi feito até aqui está armazenado na memória do computador, e só lá! E, claro, não se deve correr o risco de perder cálculos tão relevantes. Para que fiquem registrados e possam ser consultados posteriormente, deve-se salvar o trabalho, o que pode ser feito pressionando o botão "salvar" da barra de ferramentas. Pois então faça isso o quanto antes! De fato, é importante salvar o trabalho de quando em quando, de forma a recuperar o que foi feito em caso de algum acidente de percurso.

Reiniciando ...

Há situações, como a do próximo comando, em que não é mais necessário exibir o resultado na tela. Para isso, o sinal de ponto e vírgula ; deve ser substituído pelo sinal de dois pontos : , como ilustrado abaixo.
[> restart; f:=x->3.7/(25+x^2)^(1/2)*x/(1.69+x^2)^(1/2):

Gráficos!!

Surpreendentemente, o gráfico de uma função é traçado aqui da mesma forma que você deve ter aprendido na escola: primeiro, calculam-se alguns valores da função; em seguida, em um sistema de eixos, marcam-se os pontos correspondentes do gráfico; por último, ligam-se esses pontos por segmentos de reta. Esse procedimento, trabalhoso quando feito manualmente, é bastante fácil se executado pelo computador, mesmo que para uma quantidade grande de pontos. Nesse caso, os vários segmentos de reta, quando unidos, dão a impressão de que a figura formada é uma curva suave.

Esse procedimento está implementado com a rotina unirpontos , definida no comando abaixo. Observe o uso do sinal de dois pontos : (muito apropriado, diga-se de passagem!), uma vez que não é necessário que as definições sejam exibidas na tela. A "mensagem" do final é apenas uma brincadeira, para enfatizar que a rotina foi implementada com sucesso.
[> unirpontos:=proc(f1,a,b,n) local x,y,v,j,delta;
  v:=array(0..n-1):
  delta:=(b-a)/(n-1):
  for j from 0 to n-1 do x[j]:=a+j*delta:
  y[j]:=f1(x[j]): v[j]:=[x[j],y[j]] od:
  plot(v); end: `Mensagem recebida, câmbio.`;

Essa rotina será melhor compreendida futuramente, mas é instrutivo saber a função dos comandos ali incluídos, quais sejam:

• na primeira e segunda linhas definem-se o nome da rotina e das variáveis que serão utilizadas;
• na terceira linha divide-se o domínio da função em partes iguais, e define-se "delta" como o comprimento dessas partes;
• na quarta linha definem-se os pontos que dividem o intervalo, incluindo os extremos;
• na quinta linha definem-se as imagens yj dos pontos obtidos na linha anterior e os respectivos pontos (xj, yj) do gráfico da função.
• na sexta linha, finalmente, unem-se os pontos do gráfico por segmentos de reta.

O comando a seguir ilustra o uso dessa rotina para o caso da função f(x) no intervalo [0, 20], utilizando 6 pontos do gráfico da função. Note que a primeira entrada é a função cujo gráfico se quer ilustrar; a segunda e a terceira são, respectivamente, o extremo inferior e o superior do intervalo em que o gráfico será ilustrado; e a última entrada é o número de pontos com que o intervalo será subdividido.
[> unirpontos(f,0,20,6);

Exercícios

18) Copie o comando anterior e altere para 50 o número de pontos em que o intervalo será subdividido. Verifique que o resultado é uma curva muito mais suave do que a anterior.
[> unirpontos(f,0,20,50);

19) A partir do gráfico acima, selecione um subintervalo que contenha o ponto de máximo da função e esboce o seu gráfico nesse subintervalo, utilizando 10 pontos.
[> unirpontos(f,2,3,10);

20) Proceda como no exercício 19 para obter um novo subintervalo, incluído no anterior, que ainda contenha o ponto de máximo da função.
[> unirpontos(f,2.4,2.8,10);

21) Usando um procedimento análogo aos dois últimos exercícios, determine um intervalo de comprimento 0.1 que contenha o ponto de máximo da função. Inclua a sua resposta no espaço indicado abaixo. Em seguida, depois de obter essa nova estimativa, ainda melhor que a anterior, não se esqueça de salvar o seu trabalho!
[> unirpontos(f,2.5,2.6,10);

Resposta : do gráfico, a função assume o seu valor máximo no intervalo [2.5, 2.6], cujo comprimento é 0.1.

Reiniciando ...

A combinação das teclas "Shift"+"Enter" pode ser usada para mudar de linha sem executar o comando, como ilustrado a seguir.
[> restart;
  f:=x->3.7/(25+x^2)^(1/2)*x/(1.69+x^2)^(1/2):

O Comando "plot"

Esse procedimento, de "unirpontos", é tão importante que a ele se dá um nome especial. Fixando em 50 o número de pontos em que o intervalo é subdividido, a rotina unirpontos é equivalente ao comando plot , predefinido no Maple, cuja sintaxe está ilustrada a seguir:
[> plot(f(x),x=0..20);

A primeira entrada desse comando é a função cujo gráfico se quer traçar e, a segunda, indicada por x=0..20 , descreve a variação de x, o intervalo [0, 20] nesse caso. Compare o resultado desse comando com aquele do exercício 18 (olha o " B ookmark"...), e verifique que a rotina unirpontos e o comando plot produzem o mesmo resultado se o intervalo for dividido em 50 pontos. De fato, a unirpontos foi introduzida apenas para explicar como os gráficos são traçados. O plot é o comando natural para isso, uma vez que, sendo predefinido, estará disponível nas próximas atividades.

Exercícios

22) O número é indicado no Maple por Pi, com inicial maiúscula. Por exemplo, execute o comando Pi e observe que o resultado é exatamente o número . Usando essa informação e o comando plot , esboce o gráfico da função seno no intervalo [-Pi / 2, Pi /2], e verifique que sin(x) é crescente nesse intervalo. Em particular, sin(x) é crescente no intervalo [0, Pi / 2], como afirmado anteriormente.
[> Pi;
  plot(sin(x),x=-Pi/2..Pi/2);

23) Observe que, ao clicar sobre o gráfico acima, muda a barra de ferramentas no topo da tela, passando a ser uma barra própria para trabalhar com gráficos. Clique na opção "1:1" dessa nova barra para que a escala utilizada nos dois eixos seja a mesma. Em seguida, procure determinar as funções dos demais botões daquela barra.

24) Sendo crescente, a função sin(x) admite a função inversa arcsin(y). Por exemplo, como sin(Pi / 6) = 1 / 2, tem-se que arcsin(1 / 2) = Pi / 6. Verifique essa afirmação solicitando o valor de arcsin(1 / 2). Solicite ainda os valores de arcsin(-1), arcsin(0) e arcsin(sqrt(3) / 2), e procure interpretar o resultado em termos da função sin(x).
[> arcsin(1/2); arcsin(-1); arcsin(0); arcsin(sqrt(3)/2);

25) Use o comando plot para esboçar o gráfico da função arcsin(y) no intervalo [-1, 1]. Em seguida, use a opção "1:1" para melhor visualização. Do gráfico, observe que arcsin(y) é também crescente no intervalo [-1, 1].
[> plot(arcsin(y),y=-1..1);

Reiniciando ...

Pode-se acrescentar comentários em um comando, desde que precedidos do sinal #, como ilustrado abaixo.
[> #Só para lembrar que esse comando deve ser executado!
  restart: f:=x->3.7/(25+x^2)^(1/2)*x/(1.69+x^2)^(1/2):

Desafios

1) Votando a consultar o exercício 10 (olha o " B ookmark"...), verifica-se que lá foram feitas duas substituições com um só comando. Tente fazer um procedimento semelhante para esboçar os gráficos de sin(x) e cos(x) no intervalo [-Pi, Pi], mas de forma a que ambos sejam ilustrados em um mesmo sistema de coordenadas. De novo, para uma melhor visualização, clique sobre a figura e em seguida escolha a opção "1:1" na barra de ferramentas.
[> plot({sin(x),cos(x)},x=-Pi..Pi);

2) No exercício 21, foi obtida uma estimativa para a "melhor distância" do painel ao observador, mas nada ainda foi dito sobre o "melhor ângulo" com que o painel pode ser visto. Usando a estimativa já obtida, que arcsin(y) é uma função crescente e que f(x) = sin(v), obtenha uma estimativa para a medida, em radianos, do "melhor ângulo". Justifique a sua resposta no espaço a seguir.
[> arcsin(f(2.5)); arcsin(f(2.6));

Justificativa : tem-se que f(x) = sin(v), e portanto v = arcsin(sin(v)) = arcsin(f(x)). Do exercício 21, segue-se então que v está entre arcsin(f(2.5)) e arcsin(f(2.6)).

3) Os valores acima estão na forma decimal, e é importante compará-los, por exemplo, com os ângulos Pi / 6, Pi / 4 e Pi / 3. Use então o evalf para obter as expressões decimais de Pi / 6, Pi / 4 e Pi / 3.
[> evalf(Pi/6); evalf(Pi/4); evalf(Pi/3);

4) A partir dos dois últimos exercícios, verifique se o "melhor ângulo" é menor que Pi / 6, se ele está entre Pi / 6 e Pi / 4, entre Pi / 4 e Pi / 3 ou se é maior que Pi / 3.
Resposta : o melhor ângulo, que está entre arcsin(f(2.5)) e arcsin(f(2.6)), é aproximadamente igual a 0.6276294259, e portanto se encontra entre Pi / 6 = 0.5235987758 e Pi / 4 = 0.7853981635.

Fim da Atividade