Projeto de Maple - Cálculo 3

(Seção 16.3 Ex. 64, vol. 2, Swokowski)

Identificação

Professora Luciana

Turma "F", 1.º/2003

Grupo

-Gustavo Fleury - 02/23557

-Gustavo Conforto - 02/45224

-Gustavo Belo - 02/23603

Problema

Seja C o traço do gráfico de z = sqrt (36 - 9*x^2 - 4*y^2) no plano y = 2. Escreva as equações paramétricas da tangente L a C no ponto p (1, 2, sqrt(11) ). Esboce a superfície, o traço C e a reta L .

Ilustração

Primeiro vamos ilustrar o problema. A superfície z cortada pelo plano y=2, onde a interseção da superfície com o plano nos da o traço C. Execute o comando para ilustrar o problema.
[> with(plots,display,implicitplot3d):
  sup:=implicitplot3d(z^2+9*x^2+4*y^2=36,x=0..2,y=0..3,z=0..6,
     axes=normal,style=patchnogrid,grid=[10,10,10],
     lightmodel=light3,color=turquoise):
  plano:=plot3d([s,2,t],s=-1..3,t=0..5,grid=[2,2]):
  display(sup,plano);

Poda ilustrar o traço C , basta considerar y constante e igual a 2.
[> plot(sqrt(36 - 9*x^2 - 4*2^2),x=0..2);

Resolução

Vamos definir função z.
[> z:=(x,y)->sqrt (36 - 9*x^2 - 4*y^2);

Podemos considerar a inclinação da reta tangente L a C no ponto " p " como sendo a derivada parcial de z(x,y) em relação a x no ponto p . Vamos definir a derivada como sendo a fução dz, e depois calcularemos o seu valor para o ponto desejado, no caso (1,2).
[> dz:=unapply(diff(z(x,y),x),(x,y)):'dz(x,y)'=dz(x,y); i:=dz(1,2);

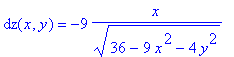
Agora já temos a inclinação i da reta tangente a C no ponto p ! Só resta calcularmos o coeficiente linear da equação da reta tangente L . Mas nós sabemos que quando x=1, z=sqrt(11), então é só montarmos uma equação para acharmos o coeficiente n.
[> n:=solve(sqrt(11)=dz(1,2)+n,n):'n'=n;

Portanto a equação da reta tangente tem a seguinte forma.
[> eq:= i*x+n: 'eq'=eq;

Agora ilustramos a reta L tangente a C , no ponto p .
[> ta:= plot(((-9)/11)*11^(1/2)*x+20/11*11^(1/2),x=0..2):
  c:= plot(sqrt(36 - 9*x^2 - 4*2^2),x=0..2):
  display(ta,c);

Substituindo x por t, podemos obter a resposta do problema, isto é, a equações paramétricas da reta L.
[> y:=2: x:=t: z:=((-9)/11)*11^(1/2)*t+20/11*11^(1/2):
  'y'=y; 'x'=x; 'z'=z;