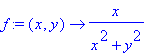
Universidade de Brasília
Departamento de Matemática

disciplina - Cálculo 3
período 2/2003
turma E
professor Célius Magalhães

PROJETO DE LABORATÓRIO

Resoluçao do Exercício 44, Seção 12.3, do livro texto (Cálculo, vol.2, de G. Thomas)

[> restart: with(student):
[>

Introdução

No cálculo de integrais duplas, muitas vezes encontramos domínios não retangulares, ou muito difíceis de se integrar. Assim, uma boa solução para este problema é a mudança de coordenadas, onde se escolhe adequadamente novas variáveis equivalentesàs anteriores, mas que adaptam o domínio a um novo formato. Assim, para cada caso existe uma mudança de variável mais apropriada.

Nosso problema aqui é calcular a integral dupla da função
[> f:=(x,y)->x/(x^2+y^2);

[>

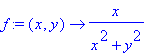
com x variando de 0 até 1, e y variando de 0 até a reta y=x/2. De fato, o problema é equivalente ao cálculo do volume abaixo do gráfico de f(x, y) no domínio descrito acima, como ilustrado a seguir.
[> plot3d(f(x,y),x=0..1,y=0..x/2,axes=normal);

[>

Esse volume pode ser representado algebricamente por
[> Doubleint('f(x,y)',y=0..x/2,x=0..1)=Doubleint(f(x,y),y=0..x/2,x=0..1);

[>

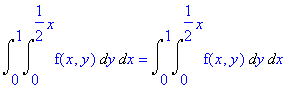
Essa integral porém está descrita em coordenadas cartesianas, e a forma de f(x,y) sugere o uso das coordenadas polares, onde mudamos a variável 'x' para r*cos(t) e 'y' para r*sin(t), onde'r' representa a distância do ponto (x,y) até a origem e 't' representa a inclinação de 'r' com a horizontal.

Desenvolvimento

A primeira parte do problema é representar graficamente a região cartesiana de integração no plano Oxy. Essa região é o conjunto de todos os pontos x e y tais que os 'x' estejam entre 0 e 1 e os 'y' estejam entre 0 e a reta y=x/2, ou seja,
[> plot3d(0,x=0..1,y=0..x/2,axes=normal,orientation=[-90,0]);

[>

Depois de representar a região de integração, é pedido no problema que seja feita a mudança de coordenadas cartesianas para coordenadas polares.

O primeiro passo então é descobrir qual é a nova função f(r,t) com as novas coordenadas.
[> powsubs(x=r*cos(t),y=r*sin(t),f(x,y));

[>

Assim já temos uma noção de como será a integral que queremos calcular. Usando o comando changevar, chegamos que
[> Doubleint(f(x,y),x=0..1,y=0..x/2)=
  changevar({x=r*cos(t),y=r*sin(t)}, Doubleint(f(x,y),x,y,D1),[t,r] );

[>

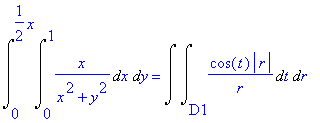
Percebemos que a mudança foi feita corretamente, e que o Maple não esqueceu o Jacobiano!

Só nos resta agora descobrir qual é o novo domínio de integração D1. Encontramos aqui a dificuldade de realizar essa mudança nos limites de integração através do Maple, e fizemos então os cálculos manualmente. Chegamos ao seguinte resultado: D1 é o conjunto dos pontos (r,t) taisque o 'r' varia de 0 até sec(t) e 't' varia de 0 até arctan(1/2).

Vamos representar então o domínio D1 graficamente, como foi pedido na terceira parte do problema:
[> plot3d(0,t=0..arctan(1/2),R=0..sec(t),orientation=[-90,0],          axes=normal,style=wireframe);

[>

Conclusão

Agora ficou tudo mais fácil! Com o novo domínio de integração resolvido e a nova função de integração pronta, o cálculo é rapidamente efetuado pelo Maple. Para resolver a integral dupla de f(x,y), usamos os comandos Doubleint e value. Assumimos r maior que zero, pois se não fizéssemos isso o Maple não dividiria abs(r) por r, e o resultado seria cheio de restrições.
[> assume(r>0);
  V:=Doubleint(f(x,y),x=0..1,y=0..x/2)=
  Doubleint(cos(t)*abs(r)/r,r=0..sec(t),t=0..arctan(1/2));

[>

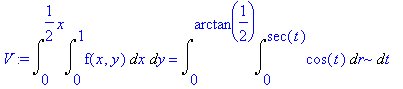
Para solicitar o valor dessa integral propriamente dito usamos o value e pronto!
[> value(rhs(V));

[>

Se não quiséssemos usar o assume, poderíamos usar o comando evalf ao invés de value, que nos traria ao mesmo resultado. [> evalf(Doubleint(cos(t)*abs(r)/r,r=0..sec(t),t=0..arctan(1/2)));

[>