BOLETÍN ELECTRÓNICO CIENTÍFICO
DEL NODO BRASILERO
DE INVESTIGADORES COLOMBIANOS
Número 2(Artículo 20), 2000
TÍTULO
ORBITAL STABILITY OF SOLITARY WAVE SOLUTIONS FOR AN INTERACTION EQUATION OF SHORT AND LONG DISPERSIVE WAVES
TIPO:
AUTOR:
Jaime Angulo Pava1angulo@ime.unicamp.br & José Fabio B. Montenegro2
IDIOMA: Inglés
DIRECCIÓN PARA CONTACTO
1IMECC, Universidade Estadual de Campinas,
Campinas, CEP 13083-970, São Paulo, Brazil
2Departamento de Matemática, Campus do Pici, Universidade Federal do Ceará,
Fortaleza, CEP 60455-000, Ceará, Brazil
ENTIDADES QUE FINANCIARON LA INVESTIGACIÓN: The second author is supported by CNPq, a Brazilian government agency that supports the development of science and technology.
PALABRAS CLAVE:
Abstract:
We study the existence and orbital stability of solitary wave solutions for an interaction equation between a long internal wave and a short surface wave in a two layer fluid. If the short wave term is denoted by
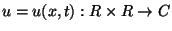 and the long wave term by
and the long wave term by
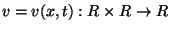 , the phenomena of interaction is described by the following equation ( Funakoshi and Oikawa (J. Phys. Soc. Japan,
, the phenomena of interaction is described by the following equation ( Funakoshi and Oikawa (J. Phys. Soc. Japan, 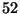 (1983), 1982-1995),
(1983), 1982-1995),
where
 ,
,
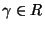 and
and 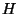 is the Hilbert transform. Via the Implicit Function Theorem we show the existence de smooth real solutions
is the Hilbert transform. Via the Implicit Function Theorem we show the existence de smooth real solutions 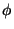 and
and 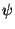 of the system
of the system
where 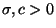 and
and  in some neighbourhood of zero. Moreover, using perturbation theory of closed operators on Hilbert spaces we show that the functions
in some neighbourhood of zero. Moreover, using perturbation theory of closed operators on Hilbert spaces we show that the functions
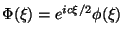 and
and
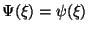 are solutions orbitally stable in
are solutions orbitally stable in
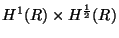 , at least when
, at least when  is negative near zero .
is negative near zero .
1. INTRODUCTION
In this work we continue our study on an interaction equation between a long internal wave and a short surface wave in a two layer fluid when the fluid depth of the lower layer is sufficiently large in comparison with the wavelength of the internal wave. The fluids are assumed with different densities, inviscid and incompressible, and their motions to be two-dimensional and irrotational. If the short wave term is denoted by
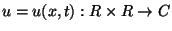 and the long wave term by
and the long wave term by
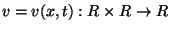 , the phenomena of interaction is described by the following nonlinear coupled system (see Funakoshi and Oikawa [14]),
, the phenomena of interaction is described by the following nonlinear coupled system (see Funakoshi and Oikawa [14]),
where  are positive constants,
are positive constants,
 and
and
 , is a linear differential operator representing the dispersion of the internal wave. Here
, is a linear differential operator representing the dispersion of the internal wave. Here 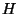 denotes the Hilbert transform defined by
denotes the Hilbert transform defined by
therefore,  is the multiplier with Fourier operator defined as
is the multiplier with Fourier operator defined as
 . Here the circumflex over a function denotes the function Fourier transform.
Several results for Eq. (1.1) have been obtained. Funakoshi and Oikawa ([14]) computed numerical solitary wave solutions. Angulo and Montenegro ([4]) proved the existence of solitary wave solutions via the concentration compactness method (Lions [18], [19]), as well as, the evenness and analyticity of these solutions. Bekiranov, Ogawa and Ponce ([6]) proved the local well-posedness theory in
. Here the circumflex over a function denotes the function Fourier transform.
Several results for Eq. (1.1) have been obtained. Funakoshi and Oikawa ([14]) computed numerical solitary wave solutions. Angulo and Montenegro ([4]) proved the existence of solitary wave solutions via the concentration compactness method (Lions [18], [19]), as well as, the evenness and analyticity of these solutions. Bekiranov, Ogawa and Ponce ([6]) proved the local well-posedness theory in
 . More precisely, if
. More precisely, if  and
and  then for any
then for any
 there exists
there exists  such that the initial value problem (1.1) admits a unique solution
such that the initial value problem (1.1) admits a unique solution
 . Moreover, for
. Moreover, for  the map
the map
 is Lipschitz continuous from
is Lipschitz continuous from
 to
to
 . For the case
. For the case  , they obtain the same results as above, but for
, they obtain the same results as above, but for  . We note that as consequence of the relations (1.2) and (1.3) below,
. We note that as consequence of the relations (1.2) and (1.3) below,  can be chosen arbitrarily large if
can be chosen arbitrarily large if
 and
and  .
For any
.
For any  , we have that the solution
, we have that the solution  preserves its
preserves its  -norm, i.e., if
-norm, i.e., if
then for any  ,
,
 . Moreover, we have the conservation laws of momentum and energy:
. Moreover, we have the conservation laws of momentum and energy:
where  is the multiplier with Fourier operator defined as
is the multiplier with Fourier operator defined as
 .
The purpose of this paper is to consider the existence and orbital stability of solitary wave solutions for Eq. (1.1) of the form
.
The purpose of this paper is to consider the existence and orbital stability of solitary wave solutions for Eq. (1.1) of the form
where we have that,
 ,
,
 , are smooth functions such that for each
, are smooth functions such that for each  ,
,
 , and
, and
 , as
, as
 ,
,  and
and
 . Thus, substituting
. Thus, substituting  as above in (1.1) we obtain the coupled system of equations
as above in (1.1) we obtain the coupled system of equations
with
 and
and  . Now, if we consider
. Now, if we consider
 , for
, for 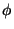 real-valued, and replace it in (1.5) finally we obtain the pseudo-differential system
real-valued, and replace it in (1.5) finally we obtain the pseudo-differential system
where
 .
We shall show the existence of smooth real solutions
.
We shall show the existence of smooth real solutions 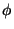 ,
, 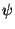 of (1.6) for
of (1.6) for  and
and  in some neighbourhood of zero via the Implicit Function Theorem. Moreover, adapting a method developed by Albert, Bona and Henry ([1]), Benjamin ([7]) and Weinstein ([23], [24]), together with some results from perturbation theory of closed operators on Hilbert spaces (Kato [16]), we shall prove that these solutions are orbitally stable in
in some neighbourhood of zero via the Implicit Function Theorem. Moreover, adapting a method developed by Albert, Bona and Henry ([1]), Benjamin ([7]) and Weinstein ([23], [24]), together with some results from perturbation theory of closed operators on Hilbert spaces (Kato [16]), we shall prove that these solutions are orbitally stable in
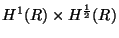 at least when
at least when  is negative near zero.
In comparison with Eq. (1.1), we consider the following system
is negative near zero.
In comparison with Eq. (1.1), we consider the following system
i.e.,  in (1.1). This model is the most typical in the theory of wave interaction and occurs when the fluid depth is sufficiently small in comparison with the wavelength of the internal wave. Eq. (1.7) also has been considered under various settings, see for example, Benney ([8],[9]), Bekiranov, Ogawa and Ponce ([5]), Grimshaw ([15]), Laurençot ([17]), Ma ([20]) and Tsutsumi and Hatano ([22]). In the particular case of the existence and stability theory of solitary wave solutions, the results are more definitive (see [17]), in the sense that solitary waves for (1.7) (
in (1.1). This model is the most typical in the theory of wave interaction and occurs when the fluid depth is sufficiently small in comparison with the wavelength of the internal wave. Eq. (1.7) also has been considered under various settings, see for example, Benney ([8],[9]), Bekiranov, Ogawa and Ponce ([5]), Grimshaw ([15]), Laurençot ([17]), Ma ([20]) and Tsutsumi and Hatano ([22]). In the particular case of the existence and stability theory of solitary wave solutions, the results are more definitive (see [17]), in the sense that solitary waves for (1.7) ( and
and  in (1.6)) are unique (up to translations) and may be computed explicitly as
in (1.6)) are unique (up to translations) and may be computed explicitly as
however, formulas of the form given in (1.8) have no known counterpart for equations of type (1.6) with  .
The plan of this paper is as follows. In section 2, we prove the existence and stability of solitary-wave solutions corresponding to values of
.
The plan of this paper is as follows. In section 2, we prove the existence and stability of solitary-wave solutions corresponding to values of  negative near zero. In the Appendix, we briefly review some results about perturbation theory of closed linear operators on Hilbert spaces necessary in the development of our work.
negative near zero. In the Appendix, we briefly review some results about perturbation theory of closed linear operators on Hilbert spaces necessary in the development of our work.
Notations. Throughout this paper we will denote by  the Fourier transform of
the Fourier transform of  , defined as
, defined as
 .
.  denotes the
denotes the  norm of
norm of  ,
,
 . In particular,
. In particular,
 and
and
 . We denote by
. We denote by  the Sobolev space of all
the Sobolev space of all  (tempered distributions) for which the norm
(tempered distributions) for which the norm
 is finite. The product norm in
is finite. The product norm in
 is denoted by
is denoted by
 .
.
 is the Riesz potential of order
is the Riesz potential of order  , and is defined by
, and is defined by
 .
.  denote the space of all bounded linear operators from
denote the space of all bounded linear operators from  into
into  . If
. If  ,
,  . If
. If  is any closed operator on
is any closed operator on  , we denote its spectrum by
, we denote its spectrum by  .
.
2. EXISTENCE AND STABILITY OF SOLITARY WAVE SOLUTIONS
For any
 define the functions
define the functions
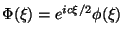 and
and
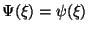 , where
, where  is a solution of (1.6). Then we said that the solitary-wave solution
is a solution of (1.6). Then we said that the solitary-wave solution
 is orbitally stable in
is orbitally stable in
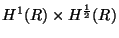 if for every
if for every  , there exists
, there exists
 such that when
such that when
 and satisfies both
and satisfies both
 and
and
 , and
, and  is the solution of (1.1) corresponding to
is the solution of (1.1) corresponding to  , then
, then
 and
and
for all
 .
The main result to be proved in this section is that stable solitary-wave solutions of (1.1) exist when
.
The main result to be proved in this section is that stable solitary-wave solutions of (1.1) exist when  and
and  is negative and near 0.
is negative and near 0.
Theorem 2.1 Let
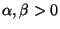 , and
, and
 , for
, for  and
and
 fixed numbers. Then there exists
fixed numbers. Then there exists  such that for each
such that for each
 , Eq. (1.6) has a solution
, Eq. (1.6) has a solution
 . Moreover, for
. Moreover, for
 and
and
 , we have that
, we have that
 is a stable solitary-wave solution of (1.1).
The proof of Theorem 2.1 will proceed by adapting a method developed by Benjamin ([7]), Albert, Bona, and Henry ([1]) and Weinstein ([24]), together with some results on spectral theory of closed linear operators on Hilbert spaces. We begin our study proving the existence of solitary-wave solutions of (1.1). Since our argument is based on the Implicit Function Theorem, we need to establish several facts on the structure spectral of the self-adjoint operator on
is a stable solitary-wave solution of (1.1).
The proof of Theorem 2.1 will proceed by adapting a method developed by Benjamin ([7]), Albert, Bona, and Henry ([1]) and Weinstein ([24]), together with some results on spectral theory of closed linear operators on Hilbert spaces. We begin our study proving the existence of solitary-wave solutions of (1.1). Since our argument is based on the Implicit Function Theorem, we need to establish several facts on the structure spectral of the self-adjoint operator on  ,
,
where  is defined in (1.8). In fact, since
is defined in (1.8). In fact, since  has a single zero and
has a single zero and
 as
as
 , we obtain from the Sturm-Liouville theory (see, [13], [10]) and perturbation theory of closed linear operators on Hilbert spaces (see, Kato [16]) that
, we obtain from the Sturm-Liouville theory (see, [13], [10]) and perturbation theory of closed linear operators on Hilbert spaces (see, Kato [16]) that  has one simple negative eigenvalue
has one simple negative eigenvalue  with eigenfunction
with eigenfunction  , a simple eigenvalue at zero with eigenfunction
, a simple eigenvalue at zero with eigenfunction  , the essential spectrum is the interval
, the essential spectrum is the interval
 , and the remainder of the spectrum of
, and the remainder of the spectrum of  consist of isolated eigenvalues of finite multiplicity. Moreover, there exists
consist of isolated eigenvalues of finite multiplicity. Moreover, there exists  such that for
such that for
 , we have that
, we have that
 .
For
.
For  , let
, let  denote the closed subspace of all even functions in
denote the closed subspace of all even functions in  . In order to prove Theorem 2.1 we have first,
. In order to prove Theorem 2.1 we have first,
Lemma 2.2 Let
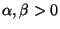 , and
, and
 , for
, for  and
and
 fixed numbers. Then there exists
fixed numbers. Then there exists  such that for every
such that for every
 , Eq. (1.6) has a solution
, Eq. (1.6) has a solution
 , and the correspondence
, and the correspondence
 defines a continuous map from
defines a continuous map from
 to
to
 . In particular, for
. In particular, for  and
and  ,
,
 converges to
converges to
 , uniformly for
, uniformly for  , where
, where  and
and  are defined as in (1.8).
Proof Without loss of generality take
are defined as in (1.8).
Proof Without loss of generality take  and
and  . Let
. Let
 and define a map
and define a map
 by
by
A calculation shows that the Fréchet derivative
 exists on
exists on
 and is defined as a map from
and is defined as a map from
 to
to
 by
by
From (1.8) it follows that for
 ,
,
 and that the operator
and that the operator
 has a one-dimensional nullspace
has a one-dimensional nullspace
 in
in
 . In fact, it follows immediately from (1.8) that
. In fact, it follows immediately from (1.8) that
 , and hence
, and hence
 . Now, we consider
. Now, we consider  such that
such that
 , then
, then  satisfies the differential equation
satisfies the differential equation
Thus,
 and therefore
and therefore
 for some
for some
 . Since
. Since
 it follows that
it follows that
 and therefore
and therefore
 is generated by
is generated by  . Since
. Since
 , it follows that
, it follows that
 is invertible. Finally, since
is invertible. Finally, since  and
and
 are continuous maps on their domains, we have from the Implicit Function Theorem that there exist a number
are continuous maps on their domains, we have from the Implicit Function Theorem that there exist a number  and a continuous map
and a continuous map
 from
from
 to
to  such that
such that
 for all
for all
 . This shows the Lemma.
. This shows the Lemma. 
Remark 2.3. Notice that for  near
near  ,
,  obtained in Lemma 2.2 is strictly positive. In fact, since
obtained in Lemma 2.2 is strictly positive. In fact, since
 as
as
 there exists
there exists  such that for each
such that for each  ,
,
 , thus
, thus
Therefore,
 for each
for each  . Now, since
. Now, since  is strictly positive and
is strictly positive and
 as
as  uniformly in
uniformly in ![$[0, M]$](img173.png) , we have that for
, we have that for  near zero
near zero
 for
for ![$x\in [0, M]$](img175.png) . Thus from the continuity of
. Thus from the continuity of  we obtain the affirmation.
The existence of the desired family of solitary-wave solutions of Eq. (1.6) established in Theorem 2.1 has now been demonstrated, and it remains to prove that these solitary waves are stable at least when
we obtain the affirmation.
The existence of the desired family of solitary-wave solutions of Eq. (1.6) established in Theorem 2.1 has now been demonstrated, and it remains to prove that these solitary waves are stable at least when  is negative and near zero. In order to show this, we need to establish some results on the spectrum of a operator associated with the solitary wave
is negative and near zero. In order to show this, we need to establish some results on the spectrum of a operator associated with the solitary wave
 , it will necessary to use some results from perturbation theory of closed linear operator on Hilbert spaces ( ch. IV-V of Kato [16]). The linear, self-adjoint, closed, and unbounded operator on
, it will necessary to use some results from perturbation theory of closed linear operator on Hilbert spaces ( ch. IV-V of Kato [16]). The linear, self-adjoint, closed, and unbounded operator on  of our interest here is given by
of our interest here is given by
where
 is a solution of (1.6) for
is a solution of (1.6) for  obtained in Lemma 2.2, the operator
obtained in Lemma 2.2, the operator
 , defined as
, defined as
 , is the inverse operator of
, is the inverse operator of
 ,
,  , defined by
, defined by
 , and
, and
 is given by
is given by
![$[\phi_\gamma\circ\Cal K_\gamma^{-1}\circ\phi_\gamma] (f)=\phi_\gamma\Cal K_\gamma^{-1}(\phi_\gamma f)$](img183.png) .
When
.
When  in (2.3) we obtain from (1.8) the operator
in (2.3) we obtain from (1.8) the operator  defined in (2.2). The following Lemma shows that for
defined in (2.2). The following Lemma shows that for  negative and near zero, the spectrum of
negative and near zero, the spectrum of  is similar to
is similar to  .
.
Lemma 2.4 There exists a constant  such that if
such that if
 , then the self-adjoint operator
, then the self-adjoint operator  on
on  , defined in (2.3) with domain
, defined in (2.3) with domain  , has the following properties:
, has the following properties:
(1)  has simple negative eigenvalue
has simple negative eigenvalue
 with eigenfunction
with eigenfunction
 , such that
, such that
 .
.
(2)  has a simple eigenvalue at zero with eigenfunction
has a simple eigenvalue at zero with eigenfunction  , and
, and
(3) There is  such that for
such that for
 , we have that
, we have that
 .
Moreover, the essential spectrum of
.
Moreover, the essential spectrum of  is the interval
is the interval
 ,
,
 as
as  , and
, and
 as
as  in
in  -norm, where
-norm, where  is the eigenfunction of the operator
is the eigenfunction of the operator  associated to the eigenvalue
associated to the eigenvalue  .
Proof Without loss of generality take
.
Proof Without loss of generality take  and
and  . First we state the following facts:
. First we state the following facts:
(a)
 ,
,
(b)
 ,
,
where
 is a metric on
is a metric on
 , the space of closed operators on
, the space of closed operators on  ( see Appendix).
Part (a) follows from Lemma 2.2. To prove part (b), first write
( see Appendix).
Part (a) follows from Lemma 2.2. To prove part (b), first write
 and
and
 , where
, where
 and
and
 . Next, note that
. Next, note that
 , with operator norm tending to
, with operator norm tending to  as
as  . In fact, first one has for
. In fact, first one has for
 that
that
Next, we estimate the second norm on the right hand side of (2.4). From the relations
and
 we have that,
we have that,
Now, for the kernel  defined by
defined by
and
 for
for  , we have that
, we have that
 . Moreover, if
. Moreover, if
 then
then
 . Thus, it follows from the Plancherel Theorem and Young's inequality that
. Thus, it follows from the Plancherel Theorem and Young's inequality that
Therefore, from the equality
 , item (a) above, and (2.5), (2.6), it follows from (2.4) that
, item (a) above, and (2.5), (2.6), it follows from (2.4) that
 as
as  . Hence,
from Theorem A.1 in the Appendix we have that
. Hence,
from Theorem A.1 in the Appendix we have that
and since
 is uniformly bounded for
is uniformly bounded for  , we have immediately the advertised result in (b).
We now turn to the proof of the Lemma. That the essential spectrum of
, we have immediately the advertised result in (b).
We now turn to the proof of the Lemma. That the essential spectrum of
 is
is
 it follows from the fact that the operator
it follows from the fact that the operator
 is relatively compact with respect to the operator
is relatively compact with respect to the operator
 , because
, because
 as
as
 ,
,
 is a bounded operator, and the essential spectrum of
is a bounded operator, and the essential spectrum of  is
is
 (see [2], [16]). Now, from Theorem A.1 in the Appendix and following similar arguments to those of the proof of Theorem 5 of Albert, Bona and Henry ([1]) we have that there exists a positive constant
(see [2], [16]). Now, from Theorem A.1 in the Appendix and following similar arguments to those of the proof of Theorem 5 of Albert, Bona and Henry ([1]) we have that there exists a positive constant  such that for each
such that for each
 , the spectrum of
, the spectrum of  have the properties established in the Lemma. Finally, since
have the properties established in the Lemma. Finally, since
 we have from Lemma 2.2 and Theorem A.1 that for
we have from Lemma 2.2 and Theorem A.1 that for  small
small
 .
. 
Remark 2.5. We note that another proof of the existence of unique negative eigenvalue (simple) and that  is a nondegenerate eigenvalue, can be given using the min-max principle. In fact, for
is a nondegenerate eigenvalue, can be given using the min-max principle. In fact, for
 , we have that
, we have that
where the last inequality is due to that
 is a positive operator and
is a positive operator and  . Thus, if
. Thus, if  and
and
 ,
,
 then from the spectral structure of
then from the spectral structure of  and item (a) in the proof of Lemma 2.4 it follows
that for
and item (a) in the proof of Lemma 2.4 it follows
that for  near zero
near zero
 . Therefore, from min-max principle ([21]) we have the advertised result.
As the stability considered here is with respect to form, i.e., up to translation in space and phase, it is propitious to introduce the following map on
. Therefore, from min-max principle ([21]) we have the advertised result.
As the stability considered here is with respect to form, i.e., up to translation in space and phase, it is propitious to introduce the following map on  (see [#!7!#], [#!11!#], [#!12!#] and [#!24!#]), namely, consider
(see [#!7!#], [#!11!#], [#!12!#] and [#!24!#]), namely, consider
 a solution of (1.6) obtained in Lemma 2.2 for
a solution of (1.6) obtained in Lemma 2.2 for  . If
. If
 and
and  is the solution to (1.1) corresponding to these initial data (see [6]), we define for all
is the solution to (1.1) corresponding to these initial data (see [6]), we define for all 
where we denote by  the bounded linear operator from
the bounded linear operator from
 to itself defined by
to itself defined by
 .
The following Lemma stating essential properties of the map
.
The following Lemma stating essential properties of the map  ( analog of Lemma 1 in [11]), will show that there exist maps
( analog of Lemma 1 in [11]), will show that there exist maps
 and
and  minimizing the function
minimizing the function
Lemma 2.6 We consider
 such that
such that
 and
and  the solution to (1.1) corresponding to this initial data. Suppose that for some
the solution to (1.1) corresponding to this initial data. Suppose that for some
 and some
and some
 , it is the case that
, it is the case that
Then, it follows that
is attained at least once in
 .
Proof It is immediate that
.
Proof It is immediate that
 is a continuous function of
is a continuous function of  on
on
 . Moreover, for any
. Moreover, for any
 , we have
, we have
The hypothesis (2.8), continuity of  , and (2.10) imply the result.
, and (2.10) imply the result.
 Next, it is established that the infimum in (2.9) is attained at points
Next, it is established that the infimum in (2.9) is attained at points  at least for
at least for  in
some interval of the form
in
some interval of the form ![$[0,T]$](img260.png) . To this end, it is sufficient to obtain condition (2.8) in such an interval. Let
. To this end, it is sufficient to obtain condition (2.8) in such an interval. Let  be such that
be such that
 . The solitary-wave solution
. The solitary-wave solution
 is globally defined. Hence from continuous dependence theory for (1.1) with
is globally defined. Hence from continuous dependence theory for (1.1) with  , established in Bekiranov, Ogawa and Ponce ([6]), we deduced that for
, established in Bekiranov, Ogawa and Ponce ([6]), we deduced that for  there exists a
there exists a  such that if
such that if
 , then the solution
, then the solution  of (1.1) corresponding to
of (1.1) corresponding to  exists at least
for
exists at least
for
 . Moreover
. Moreover
for all ![$ t\in [0,T]$](img267.png) . Now, since
. Now, since
it follows that
 , and therefore we have (2.8) because of the value of
, and therefore we have (2.8) because of the value of  just specified above. Thus, the infimum (2.9) is taken on at values
just specified above. Thus, the infimum (2.9) is taken on at values
 throughout the time-interval
throughout the time-interval ![$[0,T]$](img260.png) .
We now turn to the proof of Theorem 2.1.
Proof of Theorem 2.1, (Stability) We consider the functions
.
We now turn to the proof of Theorem 2.1.
Proof of Theorem 2.1, (Stability) We consider the functions
 and
and
 , where
, where
 is the solution of (1.6) obtained in Lemma 2.2 and
is the solution of (1.6) obtained in Lemma 2.2 and  is negative close to zero such that Remark 2.3, Lemma 2.4 are true. Moreover, we consider
is negative close to zero such that Remark 2.3, Lemma 2.4 are true. Moreover, we consider
 such that
such that
 and
and  the solution to (1.1) corresponding to this initial data.
The proof of stability is based on the continouos functional
the solution to (1.1) corresponding to this initial data.
The proof of stability is based on the continouos functional  defined on
defined on
 by
by
where  are defined by (1.2) and (1.3). We observe that for
are defined by (1.2) and (1.3). We observe that for  solution of (1.1),
solution of (1.1),
 at any time
at any time
 .
To prove (2.1), write a renormalized version of
.
To prove (2.1), write a renormalized version of  , namely,
, namely,
where
 and
and  are chosen such that the infimum (2.9) is take on at this values, at least for
are chosen such that the infimum (2.9) is take on at this values, at least for ![$ t\in [0,T]$](img267.png) . Thus, if
. Thus, if
 and
and
 the result of Lemma 2.6 together with (1.6) provide us with compatibility relations on
the result of Lemma 2.6 together with (1.6) provide us with compatibility relations on  and
and  , namely
, namely
and
for all ![$ t\in [0,T]$](img267.png) .
Now, using the representation (2.11) and (1.6) we have
.
Now, using the representation (2.11) and (1.6) we have
where  is defined as in (2.3),
is defined as in (2.3),
 is given by
is given by
and
 ,
,
 are the positive roots of
are the positive roots of
 and
and
 respectively. Now, we need to find a lower bound for
respectively. Now, we need to find a lower bound for  . The first step will be to obtain a suitable lower bound of the last term on the right-hand side of (2.14). In fact, since
. The first step will be to obtain a suitable lower bound of the last term on the right-hand side of (2.14). In fact, since
 is a bounded operator on
is a bounded operator on  ,
,  is uniformly bounded, and from the continuous embedding of
is uniformly bounded, and from the continuous embedding of  in
in  and in
and in
 , we have that
, we have that
where  and
and  are positive constants.
The estimates for
are positive constants.
The estimates for
 and
and
 are obtained in the next two Lemmas.
are obtained in the next two Lemmas.
Lemma 2.7 Consider  and near zero such that Lemma 2.4 is true. If
and near zero such that Lemma 2.4 is true. If  is defined as in (2.3), then
is defined as in (2.3), then
Proof Proof of part (a). From Lemma 2.4,  has exactly one negative eigenvalue
has exactly one negative eigenvalue
 (simple) with eigenfunction
(simple) with eigenfunction
 , such that
, such that
 for
for  near zero. Moreover, since zero is not an eigenvalue for
near zero. Moreover, since zero is not an eigenvalue for  in
in  , we have that
, we have that  when considered as an operator on
when considered as an operator on  , it does not have zero in its spectrum for values of
, it does not have zero in its spectrum for values of  sufficiently close to zero, because
sufficiently close to zero, because
 . Thus
. Thus
 is well-defined on
is well-defined on  , and from Theorem IV. 2.25 of Kato ([16]) and Lemma 2.2, it follows that the function
, and from Theorem IV. 2.25 of Kato ([16]) and Lemma 2.2, it follows that the function
 depends continuously on
depends continuously on  in the
in the  -norm. Now, since
-norm. Now, since
 and the nullspace of
and the nullspace of  is spanned by
is spanned by  , then
, then
 . Therefore by continuity
. Therefore by continuity
 for
for  near zero. Thus, as consequence of the last reasoning and Theorem A.3 in the Appendix we have that
near zero. Thus, as consequence of the last reasoning and Theorem A.3 in the Appendix we have that  for
for  in some neighbourhood of zero.
Proof of part (b). Because of part (a), we know that
in some neighbourhood of zero.
Proof of part (b). Because of part (a), we know that  . Suppose that
. Suppose that  and let
and let
 be a sequence of
be a sequence of  -functions with
-functions with  ,
,

 and
and
 as
as  .
Then, for any
.
Then, for any  , there is a natural number
, there is a natural number  such that for
such that for  ,
,
Then (2.17) implies that there is a subsequence of  , which we denote
again by
, which we denote
again by  , and a function
, and a function
 such that
such that
 weakly in
weakly in  and uniformly for each compact subset of
and uniformly for each compact subset of  . So
. So  satisfies the conditions
satisfies the conditions
 and
and
 . Moreover, from the
just mentioned properties of the sequence
. Moreover, from the
just mentioned properties of the sequence  , the decay of
, the decay of
 to zero as
to zero as
 , and that
, and that
 is a bounded operator, we have
is a bounded operator, we have
as  . Taking the limit in (2.17) as
. Taking the limit in (2.17) as  yields
yields
Since  is arbitrary and
is arbitrary and
 , it must be the case that
, it must be the case that  . It is now show that the
infimum is achieved. Indeed, weak convergence is lower semi-continuous, so
. It is now show that the
infimum is achieved. Indeed, weak convergence is lower semi-continuous, so
Now, define
 . Then,
. Then,  ,
,
 ,
,
 , and
, and
 . A consequence of the last reasoning is that there exist non-trivial critical points
. A consequence of the last reasoning is that there exist non-trivial critical points
 for the Lagrange problem,
for the Lagrange problem,
Using (2.18) and
 , it is easily seen that
, it is easily seen that  .
Taking the inner product of (2.18) with
.
Taking the inner product of (2.18) with
 , we have from equality
, we have from equality
 that
that
but the integral in (2.19) converge to
as  . Then, for
. Then, for  negative and near zero we have from (2.19) that
negative and near zero we have from (2.19) that  and therefore
and therefore
Now, taking inner product of (2.20) with
 , we have
, we have
since
 , for
, for  near zero, it follows that
near zero, it follows that  and
and
 , therefore from Lemma 2.4
, therefore from Lemma 2.4
 for some
for some  , which is a
contradiction since
, which is a
contradiction since
 is not orthogonal to
is not orthogonal to
 in
in  , for
, for  near zero. Thus, the minimum is
positive and the proof of the Lemma is completed.
near zero. Thus, the minimum is
positive and the proof of the Lemma is completed. 
Lemma 2.8 Consider  near zero such that Remark 2.3 is true. If
near zero such that Remark 2.3 is true. If
 is defined as in (2.15), then there is a positive value
is defined as in (2.15), then there is a positive value  such that
such that
Proof Because of Remark 2.3,  is strictly positive for
is strictly positive for  in some neighbourhood of zero. Moreover,
in some neighbourhood of zero. Moreover,  satisfies that
satisfies that
 , thus it follows that
, thus it follows that
 is a non-negative operator on
is a non-negative operator on  . Therefore, the infimum on the left-hand side of (2.21) is non-negative.
Suppose that
. Therefore, the infimum on the left-hand side of (2.21) is non-negative.
Suppose that  . Following the proof of part (b) in Lemma 2.7, we have that the minimum is attained at an admissible function
. Following the proof of part (b) in Lemma 2.7, we have that the minimum is attained at an admissible function  and there is
and there is
 such that
such that
Thus, as a consequence of the condition
 , we have
, we have  . Now, taking the inner product of
(2.22) with
. Now, taking the inner product of
(2.22) with  it is deduced that
it is deduced that
and therefore  , because
, because
 for
for  near zero. Then, since
near zero. Then, since  is the ground state for
is the ground state for
 , it follows that
, it follows that
 for some
for some  , which is a contradiction since
, which is a contradiction since
 is not orthogonal to
is not orthogonal to
 in
in  . This completes the proof.
. This completes the proof.  We now again turn to the proof of Theorem 2.1. Attention is now turned to estimating the terms
We now again turn to the proof of Theorem 2.1. Attention is now turned to estimating the terms
 and
and
 in (2.14), where
in (2.14), where  and
and  satisfy the relations (2.12) and (2.13) respectively. Thus, from Lemma 2.8, there exists
satisfy the relations (2.12) and (2.13) respectively. Thus, from Lemma 2.8, there exists  such that
such that
Then from the particular form of the operator
 it follows that there is
it follows that there is  such that
such that
Now, suppose without loss of generality that
 . We write
. We write
 , where
, where
 . Then, from (2.13) and the positivity of operator
. Then, from (2.13) and the positivity of operator
 it follows that
it follows that
 , and therefore from Lemma 2.7, it follows
, and therefore from Lemma 2.7, it follows
 . Thus, from hypothesis
. Thus, from hypothesis
 ,
,
 , Cauchy-Schwartz inequality and the specific form of the operator
, Cauchy-Schwartz inequality and the specific form of the operator  , we obtain
, we obtain
with  .
Finally, collecting the results in (2.16),(2.24),(2.25) and substituting them in (2.14), we obtain
.
Finally, collecting the results in (2.16),(2.24),(2.25) and substituting them in (2.14), we obtain
where  . Therefore, from standard arguments ( Bona [11], Weinstein [24]) for
. Therefore, from standard arguments ( Bona [11], Weinstein [24]) for  sufficiently small there is a
sufficiently small there is a
 such that if
such that if
 and
and
 then
then
for
 .
Now, it follows from (2.14) and from the above study of
.
Now, it follows from (2.14) and from the above study of  that
that
Thus, from (2.27) and the equivalence of the norms
 and
and
 we obtain (2.1). We have thus proved that
we obtain (2.1). We have thus proved that
 is stable relative to small perturbation which preserve the
is stable relative to small perturbation which preserve the  norm of
norm of  .
Now we discuss the stability relative to general perturbation. First,we remark that from Lemma 2.2 we have that for
.
Now we discuss the stability relative to general perturbation. First,we remark that from Lemma 2.2 we have that for
the correspondence
 defines a continuous map from
defines a continuous map from
 to
to
 . Moreover,
. Moreover,
 satisfies the system
satisfies the system
Let  be such that
be such that
 and
and
 , then we can find
, then we can find  and
and
 such that
such that
 and
and
 , where
, where
 . Thus, we have that the functions
. Thus, we have that the functions
satisfy the system
and
 . Moreover, from the choice of
. Moreover, from the choice of  it follows that
it follows that
 (see [3] pg. 17 for a similar situation). Therefore, applying the preceding theory to the case of
(see [3] pg. 17 for a similar situation). Therefore, applying the preceding theory to the case of
 and
and
 we have (2.1) for
we have (2.1) for
 . Theorem 2.1 is now established
. Theorem 2.1 is now established 
APPENDIX
In this Appendix, we state some facts from perturbation theory of closed linear operators on Hilbert spaces that we have used along this work (see Kato [16] for details).
We consider
 the Hilbert space with norm defined by
the Hilbert space with norm defined by
 , and for any closed operator
, and for any closed operator  on
on  with domain
with domain  , its graph,
, its graph,
 . Then a metric
. Then a metric
 on
on
 , the space of closed operators on
, the space of closed operators on  , may be defined as follows: for any
, may be defined as follows: for any
 ,
,
where  and
and  are the orthogonal projections on
are the orthogonal projections on
 and
and  , and
, and
 denotes the operator norm on the space of bounded operators on
denotes the operator norm on the space of bounded operators on
 .
.
Theorem A.1 Let
 , and suppose
, and suppose  is a bounded operator on
is a bounded operator on  with operator norm
with operator norm
 . Then
. Then
Theorem A.2 Let
 and let
and let  denote an open subset of the complex plane whose boundary is a smooth contour
denote an open subset of the complex plane whose boundary is a smooth contour  . Suppose that
. Suppose that
 and
and
 consists of a finite number of eigenvalue of
consists of a finite number of eigenvalue of  , each with finite (algebraic) multiplicity. Then there exists
, each with finite (algebraic) multiplicity. Then there exists  such that if
such that if
 and
and
 , then
, then
 consists of a finite number of eigenvalue of finite multiplicity, the sum of their multiplicities being equal to the sum of the multiplicities of the eigenvalues of
consists of a finite number of eigenvalue of finite multiplicity, the sum of their multiplicities being equal to the sum of the multiplicities of the eigenvalues of  in
in  .
In particular, suppose
.
In particular, suppose
 consists of a single, simple eigenvalue
consists of a single, simple eigenvalue  with eigenfunction
with eigenfunction  . If
. If  is a sequence in
is a sequence in
 such that
such that
 as
as  , then for
, then for  large,
large,
 consists of a single simple eigenvalue
consists of a single simple eigenvalue  , and
, and
 as
as  . Moreover, there is an eigenfunction
. Moreover, there is an eigenfunction  associated to
associated to  such that
such that  as
as  in
in  -norm.
Finally, the next result is discussed in Weinstein [23].
-norm.
Finally, the next result is discussed in Weinstein [23].
Theorem A.3 Let  be a self-adjoint operator on
be a self-adjoint operator on  having exactly one negative eigenvalue
having exactly one negative eigenvalue  with corresponding ground-state eigenfunction
with corresponding ground-state eigenfunction  and let
and let
 . Assume
. Assume
 and that
and that
If
 , then it must be the case that
, then it must be the case that  .
.
REFERENCES
- [1]
J. P . Albert, J .L . Bona and D. Henry, Sufficient conditions for stability of solitary-wave solutions of model equations for long waves
Physica D
24
1987
343-366
- [2]
J. P. Albert, J. L. Bona and J.-C. Saut, Model equations for waves in stratified fluids
Proc. Soc. Lond.
A 453
1997
1233-1260
- [3]
J. Angulo, J. L. Bona, F. Linares, and M. Scialom, On the structure of singularities in solutions of the nonlinear Schrödinger equation for the critical case,
 , in `` Nonlinear Theory of Generalized Functions, '' Vol. 401
Research Notes in Mathematics,
Chapman& Hall/CRC
1999
, in `` Nonlinear Theory of Generalized Functions, '' Vol. 401
Research Notes in Mathematics,
Chapman& Hall/CRC
1999
- [4]
J. Angulo and J. F. Montenegro, Existence and evenness of solitary wave solutions for an equation of short and long dispersive waves, submitted
- [5]
D. Bekiranov, T. Ogawa and G. Ponce, On the well-posedness of Benney's interaction equation of short and long waves
Advances Diff. Equations, in press
- [6]
D. Bekiranov, T. Ogawa and G. Ponce, Interaction equation for short and long dispersive waves
J. Funct. Anal.
158
1998
357-388
- [7]
T. B. Benjamin, The Stability of solitary waves
Proc. Roy. Soc. London A
338
1972
153-183
- [8]
D. J. Benney, Significant interactions between small and large scale surface waves
Stud. Appl. Math.
55
1976
93-106
- [9]
D. J. Benney, A general theory for interactions equation between short and long waves
Stud. Appl. Math.
56
1977
81-94
- [10]
F. A. Berezin and M. A. Shubin, `` The Schrödinger equation ''
Kluwer Academic
1991
- [11]
J. L. Bona, On the stability theory of solitary waves
Proc. Roy. Soc. London A
344
1975
363-374
- [12]
T. Cazenave and P. L. Lions, Orbital stability of standing waves for some nonlinear Schrödinger equations
Comm. Math. Phys.
85
1982
549-561
- [13]
E. A. Coddington and N. Levison, `` Theory of Ordinary Differential Equations ''
McGraw-Hill
New York
1955
- [14]
M. Funakoshi and M. Oikawa, The resonant interaction between a long internal gravity wave and a surface gravity wave packet
J. Phys. Soc. Japan
52
1983
1982-1995
- [15]
R.H.J. Grimshaw, The modulation of an internal gravity-wave packet and the resonance with the mean motion
Stud. Appl. Math.
56
1977
241-266
- [16]
T. Kato, `` Perturbation Theory for Linear Operators '', 2nd ed.
Springer - Verlag
New York
1976
- [17]
Ph. Laurençot, On a nonlinear Schrödinger equation arising in the theory of water waves
Nonlinear Anal. TMA
24
1995
509-527
- [18]
P.L. Lions, The concentration-compactness principle in the calculus of variations. The locally compact case, part 1
Ann. Inst. H. Poincaré, Anal. Non linéare
1
1984
109-145
- [19]
P.L. Lions, The concentration-compactness principle in the calculus of variations. The locally compact case, part 2
Ann. Inst. H. Poincaré, Anal. Non linéare
4
1984
223-283
- [20]
Y-C. Ma, The complete solution of the long-wave-short-wave resonance equations
Stud. Appl. Math.
59
1978
201-221
- [21]
M. Reed and B. Simon, `` Methods of Modern Mathematical Physics: Analysis of Operator, '' Vol. IV
Academic Press
New York
1978
- [22]
M. Tsutsumi and S. Hatano, Well-posedness of the Cauchy problem for Benney's first equations of long wave short wave interactions
Funkcialaj Ekvacioj
37
1994
289-316
- [23]
M. I. Weinstein, Modulation stability of ground states of nonlinear Schrödinger equations
SIAM J. Math. Anal.
16
1985
472-491
- [24]
M. I. Weinstein, Liapunov stability of ground states of nonlinear dispersive evolutions equations
Comm. Pure Appl. Math
39
1986
51-68
BECNBIC,2(20)2000