Atividades do Colóquio
Informações gerais
Festival de Matemática
Mesas Redondas
Minicursos
Plenárias
Sessões
Atividades Culturais
Todas as plenárias, mesas-redondas e palestras do festival de matemática terão intérprete de libras.
Durante o colóquio enviaremos mensagens se avisos sobre as atividades também em grupos de WhatsApp. Seguem os links para aqueles que quiserem receber informações por esse meio de contato.
VI Colóquio de Mat - 1:
https://chat.whatsapp.com/IRpxh3Juj4b7yZD8vbCCiDVI Colóquio de Mat - 2:
https://chat.whatsapp.com/BWmO4ZxX4ylIKcYVp7olX0VI Colóquio de Mat - 3:
https://chat.whatsapp.com/G5uMZabE8uAAnMJDPLU9qIVI Colóquio de Mat - 4:
https://chat.whatsapp.com/FDvbpOMUovU4KYgUqHrSp6VI Colóquio de Mat - 5:
https://chat.whatsapp.com/JrySDXA4pbk0Mag2paeTFAFestival de Matemática
x
Construção da Reta Real: dos livros do Ensino Médio à realidade do que é matematicamente possível (Geometria Grega+Livros didáticos+Arte+Sala de Aula)
Período:
17 de maio de 2021, das 17h30 às 18h30.Link de transmissão:
https://youtu.be/rr3JRvoX3-0Palestrante:
Daniel Cordeiro (UFCG)
Resumo:
Os livros do Ensino Médio sempre trazem a construção da reta numérica real e expõem a equivalência dessa reta com o conjunto dos números reais. Com esse procedimento, fica-se com a impressão de que todo número real pode ser marcado na reta real. Será esse fato realmente verdade? Pode-se marcar qualquer número na reta real? Como marcar certos números, bem pouco comuns? O que usar para fazer isso? A palestra almeja “responder” essas perguntas e incitar outras mais instigantes, cujas respos-tas requerem bem mais Matemática do que o Ensino Médio pode prover! Esse fato deve ser encarado como estímulo à uma formação acadêmica sólida de futuros professores de Mate-mática. Nesse bate-papo entram os antigos gregos, arte, animações e atividades para sala de aula!
x
Matemática: da sala de aula à divulgação científica
Período:
17 de maio de 2021, das 18h30 às 19h30.Link de transmissão:
https://youtu.be/m8P1jSgL3yEPalestrante:
Julia Jaccoud
Resumo:
Nesta conversa, Julia compartilhará sobre sua trajetória, projetos que está envolvida e instigará reflexões sobre o cenário da divulgação científica.
x
Mesa Redonda da Sociedade Brasileira de Matemática
Período:
17 de maio de 2021, das 16h30 às 17h30.Link de transmissão:
https://youtu.be/pd15AqjYkWgParticipantes da Mesa:
Christina Brech (USP)
Daniel Gonçalves (UFSC)

Jaqueline Mesquita (UnB) - Mediadora
Paolo Piccione (USP)

Walcy Santos (UFRJ)

x
Mesa Redonda: “Mídias sociais em prol da diversidade: realidade ou utopia?”
Período:
18 de maio de 2021, das 16h30 às 18h30.Link de transmissão:
https://youtu.be/IJHyhaqrLlwParticipantes da Mesa:
Carolina Tokarski (IPEA) - Mediadora
Camila Lainetti (USP)

Lola Aronovich (UFC)

Nádia Junqueira (UNICAMP)

Resumo:
A proposta da mesa, que ocorre em homenagem ao 12 de maio, dia em que celebramos as mulheres na matemática, busca trazer um olhar para questões de gênero na matemática. Vivemos um tempo em que as mídias sociais exercem forte influência no tecido social. A popularização em massa da internet a partir dos anos 2000 promoveu um amálgama entre o mundo físico e o mundo digital, de onde são publicizados protestos, debates e informações, sem nenhum controle centralizado. Esta configuração propicia um espaço fértil para a liberdade de expressão, que pode ser usado tanto para espalhar mentiras quanto para dar visibilidade para as minorias. Testemunhamos recentemente a fragilidade das democracias diante da produção em massa de conteúdos falsos durante períodos eleitorais. A “cultura do cancelamento” nas redes também é um fenômeno que revela pontos críticos de questões de raça e gênero estruturais. Os movimentos em prol dos direitos das minorias ganham forças nas redes, através do que tem sido chamado de “ciberativismo”.Convidamos para compor esta mesa especialistas nas temáticas que estudam questões de gênero e suas interseccionalidades e o impacto das mídias sociais, para refletirmos como estas últimas afetam as estruturas sociais, a partir de um olhar multidisciplinar.
x
Mesa Redonda para Mulheres na Ciência: "A força feminina na matemática"
Período:
18 de maio de 2021, das 19h00 às 20h30.Link de transmissão:
https://youtu.be/8qkk7eoUXvUParticipantes da Mesa:
Cristina Garcia (Diretora Científica da L'Oréal Brasil)
Jaqueline Godoy Mesquita (UnB)
María Amelia Salazar (UFF)

Susanne Maciel (UnB) - Mediadora

Paolo Piccione (USP) - Abertura da Mesa

x
Soluções de viscosidade e problemas variacionais
Período:
17, 18 e 19 de maio de 2021, das 14h às 16h.Link do Zoom:
https://us02web.zoom.us/j/84185855159?pwd=UkFoR2pGdzNUV0psMnZ6UWFZT2FrZz09ID da reunião: 841 8585 5159
Senha: 458518
Professor:
Edgard Pimentel (PUC/Rio)
Resumo:
O mini-curso trata de soluções de viscosidade e explora suas conexões com os problemas variacionais. A princípio, esta ligação soa artificial. Entretanto, alguns operadores fundamentais para a Análise admitem tanto soluções viscosas como soluções fracas distribucionais. Mais ainda, em alguns contextos as duas noções coincidem. Este é o caso, por exemplo, do operador Laplaciano e do operador p-Laplaciano. Uma pergunta fundamental se coloca: é possível abordar problemas variacionais a partir das técnicas das soluções de viscosidade (intrinsicamente não-variacionais)? A resposta, positiva, é o tema deste curso. Vamos introduzir a teoria de soluções de viscosidade contínuas e suas principais propriedades (e.g. princípios do máximo e da comparação, existência de soluções e desigualdade de Harnack), culminando com a regularidade das funções na classe das soluções viscosas. Em seguida, vamos discutir alguns exemplos importantes que conectam o mundo variacional e a teoria de soluções de viscosidade. Estes incluem o operador Laplaciano e o operador p-Laplaciano, e os sistemas chamados mean-field games.Público-alvo:
Estudantes de graduação e ós-graduação com interesse em EDPs; jovens doutores e pesquisadores interessados no tema.Pré-requisitos:
O principal pré-requisito é um curso de equações diferenciais parciais em nível básico, o que corresponde aos Capítulos 2 e 3 do livro-texto Partial Differential Equations, de Lawrence C. Evans. Os co-requisitos do curso envolvem noções básicas de cálculo e algum informação sobre espaços de funções.
x
Curvas de largura constante
Período:
17, 18 e 19 de maio de 2021, das 14h às 16h.Link do Zoom:
https://us02web.zoom.us/j/83837136551?pwd=clZHUFBKU3h4WVlnUFpLNHBHVzAyQT09ID da reunião: 838 3713 6551
Senha de acesso: 263501
Professores:
Arlandson Matheus (UEPB)
Emanuela Régia (UEPB)

Resumo:
A largura de uma curva planar, numa dada direção, é a largura mínima entre as faixas que contém a curva e que são limitadas por retas ortogonais a essa direção. Assim, a largura de uma curva pode não ser a mesma em todas as direções. Neste minicurso, entretanto, como seu título não se esforça por esconder, trataremos de curvas de largura constante, isto é, curvas cuja largura não muda com a direção, como é o caso do círculo e do triângulo de Reuleaux. Aproveitaremos o ensejo para introduzir o estudo de curvas no plano sob a perspectiva da Geometria Diferencial, o que nos permitirá provar que o perímetro de uma curva convexa de largura constante é igual ao da circunferência com a mesma largura (teorema de Barbier), dentre outras propriedades da classe de curvas de que nos ocuparemos.Público-alvo:
Estudantes de graduação e pós-graduação em Matemática ou áreas afins, professores de Matemática do ensino básico e qualquer pessoa que tenha interesse em Geometria Diferencial.Pré-requisitos:
Cálculo de funções reais de uma e de várias variáveis reais e Álgebra Linear.
x
O atrator geométrico de Lorenz e suas variantes
Período:
17, 18 e 19 de maio de 2021, das 14h às 16h.Link do Zoom:
https://us02web.zoom.us/j/81113308988?pwd=dUZkdG5lM3FiRVpOZ2o1UHFINDJ3QT09ID da reunião: 811 1330 8988
Senha de acesso: 291127
Professor:
Maria José Pacífico (UFRJ)
Resumo:
Nos anos 60 E. Lorenz exibiu um sistema de trˆes equa¸c˜oes diferenciais para modelar a evolução a longo termo do clima. Este sistema, tem um ponto de equilíbrio robustamente acumulado por trajetórias regulares do sistema e apesar de ser constituído por equações simples (polinomiais de grau 2), Lorenz não conseguiu exibir uma solução explícita. A razão desta resistência é tanto conceitual como numérica: do ponto de vista conceitual, não é hiperbólico e do ponto de vista numérico, há acúmulo de erros quando a trajetória se acumula do equilíbrio. No entanto, Lorenz percebeu que as soluções deste sistema deveriam depender sensivelmente das condições iniciais. E conjecturou que sua solução deveria conter um atrator de volume zero, sensível com respeito ás condições iniciais. Nos anos 70, Gugkenheimer e Williams, introduziram o atrator geométrico de Lorenz, que satisfazia todas as condições e conjecturas dadas por Lorenz. E eu pretendo falar neste minicurso exatamente sobre o atrator geométrico de Lorenz, suas propriedades básicas e alguns resultados mais recentes sobre este tipo de atrator.Pré-resquisitos:
Este será um curso de nível médio e pretendo fazer exposições explorando bastante a geometria por trás das construções. Assim, estudantes com alguma noção de fluxos e campos de vetores e com uma boa visão geométrica serão capazes de acompanhar os temas que irei desenvolver. Vou explorar mais a geometria dos problemas que a parte aritmética, dando apenas um sketch das provas dos resultados. Em particular, a primeira aula será bem elementar, com motivação e descrição do tema. Dependendo da audiência posso entrar mais na parte técnica e transformá-lo em avançado.
x
Tópicos em Dinâmica Aritmética
Período:
17, 18 e 19 de maio de 2021, das 14h às 16h.Link do Zoom:
https://us02web.zoom.us/j/86986127340?pwd=amEvdjh1a2xXeXZucjczcVgvV05idz09ID da reunião: 869 8612 7340
Senha de acesso: 063604
Professor:
Lucas Reis (UFMG)
Resumo:
Este minicurso visa introduzir o estudo de iterações de funções sobre estruturas algébricas (finitas). Vamos discutir alguns conceitos e resultados básicos do tema, e passar por dois exemplos interessantes: as funções monomiais sobre grupos abelianos finitos e as tranformações lineares sobre espaços vetoriais de dimensão finita sobre um corpo finito.Público-alvo:
Alunos de pós graduação em Matemática e alunos do final do curso de graduação em matemática.Pré-requisitos:
Conhecimento básico em álgebra.Material do Minicurso:
x
Algumas variações, generalizações e aplicações do teorema do valor médio de Lagrange
Período:
19, 20 e 21 de maio de 2021, das 16h30 às 18h30.Link do Zoom:
https://us02web.zoom.us/j/82323577707?pwd=WHRMc3h1R2xhNUQwV1o5eW5QcUY4dz09ID da reunião: 823 2357 7707
Senha de acesso: 654217
Professor:
German Jesus Lozada (IBILCE/UNESP)
Resumo:
Sabemos que os teoremas do tipo valor médio são resultados básicos da Análise Matemática. Estes teoremas se destacam por sua simplicidade e aplicabilidade em outras áreas, como em Física e Economia por exemplo. O primeiro contato de nossos alunos dos cursos de graduação em Matemática ou de Engenharia com os teoremas do tipo valor médio é em um curso de cálculo diferencial e integral ou em um primeiro curso de análise real. Neste minicurso apresentaremos alguns teoremas do tipo valor médio que não são estudados em disciplinas clássicas de cálculo e análise matemática. Também vamos ver algumas variações, generalizações e aplicações do teorema de valor médio de Lagrange.Público-alvo:
Estudantes de graduação.Pré-requisitos:
Os pré-requisitos mínimos para este minicurso são conhecimentos básicos de continuidade, diferenciabilidade e integração de funções definidas em um intervalo [a,b] mda reta e que tomam valores em R.Material do Minicurso:
x
Geometria Fractal
Período:
19, 20 e 21 de maio de 2021, das 16h30 às 18h30.Link do Zoom:
https://us02web.zoom.us/j/83700106746?pwd=WUFndWlqdFFPZlRBNFNUbjlVYXpyUT09ID da reunião: 837 0010 6746
Senha de acesso: 393820
Professor:
Katrin Gelfert (UFRJ)
Resumo:
``Nuvens não são esferas, montanhas não são cones, litorais não são círculos. A casca não é lisa - e o relâmpago não encontra seu caminho reto.'' Nesta frase, Benoît Mandelbrot nos alerta que formas geométricas clássicas - como linhas suaves ou retângulos - não são de forma alguma comuns na natureza. Pelo contrário, muitas vezes observamos formas geométricas ásperas ou fragmentadas que podem ser divididas em partes, onde cada uma delas é (aproximadamente) uma cópia em tamanho reduzido do todo. Esta observação nos leva ao conceito de autosimilaridade, propriedade bastante comum em fractais. Muitos exemplos importantes de fractais estão associados a sistemas de funções iteradas (IFS em inglês). Uma aspecto importante na geometria fractal é a descrição e caracterização de como um objeto re-escala com o seu tamanho. Dimensões fractais são ferramentas que ajudam na quantificação desta propriedade. Além do seu interesse intrínseco, a geometria fractal se caracteriza pelas múltiplas relações com outras áreas como geometria ou teoria de números, dentre outros. Neste minicurso apresentaremos as definições e as propriedades principais da dimensão de Hausdorff e da dimensão de Minkowski (``box-counting''). Discutiremos algumas técnicas para calcular estas dimensões fractais e veremos alguns exemplos paradigmáticos. Estudaremos o denominado princípio de distribução de massa que fornece estimativas da dimensão de Hausdorff a base de estimativas de dimensões locais de medidas. Finalmente, consideramos atratores de sistemas de funções iteradas e revisamos resultados clássicos e recentes para determinar suas dimensões.Pré-requisitos:
Conceitos básicos de análise e da teoria de medida.
x
Alunos digitais: os desafios e possibilidades do ensino da matemática à luz da BNCC
Período:
19, 20 e 21 de maio de 2021, das 16h30 às 18h30.Link do Zoom:
https://us02web.zoom.us/j/85706379624?pwd=M1U0OGNoUkRYekd1UDNzMGxUc1Rsdz09ID da reunião: 857 0637 9624
Senha de acesso: 187302
Professor:
Giancarlo Secci de Souza Pereira (Rede Estadual de Ensino do Pará)
Cristiane Ruiz Gomes (UFPA)

Resumo:
O objetivo deste minicurso é apresentar atividades de diferentes tópicos da matemática utilizando Tecnologias Digitais da Informação e Comunicação (TDIC) que possam auxiliar o professor na apresentação, desenvolvimento e aprofundamento desses conceitos, bem como as possibilidades que essas ferramentas digitais proporcionam e que impactos trazem ao processo de construção do conhecimento. Nesse contexto, aponta-se algumas das características dos alunos desta época e busca-se saber, através da análise do Plano Nacional de Educação (PNE), das Orientações Curriculares para o Ensino Médio (OCEM) e da Base Nacional Comum Curricular (BNCC), como a legislação educacional vigente tem tratado esse tema. Para a obtenção dos resultados dessa proposta de minicurso direcionamos as pesquisas as palavras-chaves: tecnologias digitais, fluxogramas, programação educativa e recursos pedagógicos digitais. Tomou-se como base teórica o trabalho de Pereira (2019) e os documentos oficiais citados.Público-alvo:
Este minicurso é destinado aos que desejam conhecer e aprofundar seus estudos a cerca do ensino da Matemática auxiliada por TDIC com base nos documentos oficiais vigentes (PNE, OCEM, BNCC), em especial, estudantes de licenciatura em matemática, pedagogia e professores da educação básica.Pré-requisitos:
Não possui.
x
Jogos Combinatórios e Números Surreais
Período:
19, 20 e 21 de maio de 2021, das 16h30 às 18h30.Link do Zoom:
https://us02web.zoom.us/j/86542060312?pwd=cVpKK2lHN3RaaWszM1VlejRpa21ydz09ID da reunião: 865 4206 0312
Senha de acesso: 128258
Professor:
Ralph Teixeira (UFF)
Resumo:
Vamos jogar NIM? Em uma mesa, há n pilhas de palitos, com x_1, x_2, x_3,... e x_n palitos, respectivamente. Você e um amigo alternam suas jogadas; na sua vez, você pode escolher a pilha que quiser, e retirar o número (positivo) de palitos que desejar daquela pilha (na vez dele, ele é que escolhe, é claro). Quem tirar o último palito ganha. Como determinar a estratégia vencedora para este jogo?NIM é um exemplo de jogo combinatório – jogos sequenciais nos quais ambos os jogadores têm informação completa (em particular, jogos combinatórios não têm o elemento de sorte). Resolver um jogo combinatório significa determinar quem o vence (supondo que ambos os jogadores jogam sempre da melhor maneira possível) e qual a estratégia vencedora a cada lance, o que pode ser feito (em teoria!) analisando completamente a árvore de opções do jogo.
Neste minicurso apresentaremos o início da teoria dos jogos combinatórios (capítulos iniciais de [1]), que cria ferramentas mais poderosas do que a "simples" análise direta de árvores. Começaremos pelo jogo Hackenbush (“desmata-mata”); cada posição deste jogo define um número (por um processo similar à construção dos reais via cortes de Dedekind). Veremos como computar e somar tais números. Vale a pena notar que esta construção engloba os números reais e vários outros, levando ao conjunto dos números surreais (incluindo números infinitesimais e infinitos, que serão apenas citados brevemente).
Em seguida, passaremos a analisar Jogos Imparciais como o NIM. As posições deste jogo levam à construção dos nímeros (denotados *1, *2, *3, ...). Aprenderemos a somá-los e utilizá-los para resolver rapidamente vários jogos imparciais de dois jogadores – frequentemente sem a necessidade de computadores! Enfim, apresentaremos o Teorema de Sprague-Grundy: “Todo jogo normal imparcial finito (com dois jogadores) é equivalente a um nímero”.
Tópicos:
1. Introdução: Jogos Combinatórios e suas Árvores.
2. Jogos positivos, negativos, nulos e “confusos com zero”.
3. Blue-Red Hackenbush e seus valores.
4. Calculando o número {a,b,c,...|d,e,f,...} -- a Regra da Simplicidade.
5. Somando e comparando jogos.
6. NIM, Nímeros e o Teorema de Sprague-Grundy.
Público-alvo:
Alunos e pesquisadores em matemática interessados em (i) resolver alguns jogos simples e/ou (ii) conhecer um corpo ordenado que contém todos os outros corpos ordenados como seus subcorpos.Pré-requisitos:
Apenas vontade de pensar logicamente.
x
Uma Introdução ao Cálculo Estocástico com Aplicações em Finanças Quantitativas
Período:
19, 20 e 21 de maio de 2021, das 16h30 às 18h30.https://us02web.zoom.us/j/84080156084?pwd=YnY2MlM0MDhGcGcwaFNCT241N1JxZz09
ID da reunião: 840 8015 6084
Senha de acesso: 197807
Professor:
Yuri Saporito (FGV)
Resumo:
Finanças Quantitativas nasceu em 1900 com o artigo Theory of Speculation de Louis Bachelier. Um dos fatos mais interessantes desse acontecimento foi o desenvolvimento de um dos mais importantes objetos matemáticos, o movimento Browniano. Desde esse início, passando pela prova de sua existência, em 1932 por Robert Wiener, e pela criação do Cálculo de Itô em 1942, o movimento Browniano se consolidou como uma das mais importantes ideias em Matemática Aplicada. Uma das áreas de sua aplicação mais bem sucedidas é Finanças Quantitativas, que serviu também, de certa forma, como o berço da teoria. Um segundo nascimento da área, em tempos mais recentes, foi a publicação do artigo de Fisher Black e Myron Scholes em 1973. Neste minicurso, irei introduzir o movimento Browniano e o Cálculo de Itô com o rigor compatível de um aluno de graduação que saiba probabilidade. No final, iremos exemplificar o uso dessa técnica tão importante no problema de apreçamento de derivativos financeiros estudado no paper de Black e Scholes.Pré-requisitos:
Probabilidade (nível graduação).Material do Minicurso:
x
EDPs, problemas de fronteira livre e suas teorias de regularidade
Horário:
18 de maio de 2021, das 10h às 11h.Link de transmissão:
https://youtu.be/HFtUV2XwEPYProfessor:
João Vitor da Silva (UNICAMP)Resumo:
Inúmeros modelos governados por processos difusivos aparecem naturalmente na formulação matemática de uma série de fenômenos em ciências puras e aplicadas na forma de certas EDPs (elípticas e parabólicas). Por tal razão, compreender suas teorias de regularidade intrínsecas (versões local e global) desempenha um papel fundamental na análise de problemas oriundos da biologia, ciência de materiais, dinâmica de fluidos, física-matemática, geometria diferencial dentre outras. De um ponto de vista aplicado, tais estudos ajudam a estabelecer resultados de classificação e comportamento de soluções de tais EDPs. Não obstante, quando tais processos difusivos envolvem mudanças descontínuas e múltiplas leis emergem em regiões a priori desconhecidas, novas dificuldades matemáticas tomam lugar. Tais fenômenos dizem respeito ao que hoje conhecemos como problemas de fronteira livre. Estes problemas e suas correspondentes análises matemáticas envolvidas em solucioná-los têm promovido inúmeros avanços na teoria de EDPs (elípticas e parabólicas) nas últimas décadas com uma vasta gama de aplicações. Portanto, nossa palestra tratará de revisitar o estado da arte dessas duas áreas da Análise matemática contemporânea apresentando os avanços mais recentes das mesmas no que diz respeito a suas teorias de regularidade.
x
Ciclos limite e aplicação em Sistemas Dinâmicos Descontínuos
Horário:
20 de maio de 2021, das 11h às 12h.Link de transmissão:
https://youtu.be/9uCK1et_K3UProfessor:
Durval José Tonon (UFG)
Resumo:
Sistemas Dinâmicos Descontínuos é uma recente subárea de Sistemas Dinâmicos, tendo uma formalização matemática mais sólida a partir dos anos 80 através de trabalhos de matemáticos da antiga União Soviética. Nessa palestra vamos tratar do problema de exibir cotas para o número máximo de ciclos limite para campos lineares por partes do plano e no espaço. Aplicaremos a teoria de Sistemas Dinâmicos Descontínuos com o intuito de obter respostas sobre a estabilidade dos sistemas que governam a dinâmica de tratamentos da AIDS.
x
A Curvatura média e suas primas de ordens mais altas
Horário:
18 de maio de 2021, das 11h às 12h.Link de transmissão:
https://youtu.be/9iK-e7fnKLYProfessor:
Maria Fernanda Elbert (UFRJ)Resumo:
Utilizando dois problemas clássicos como fios condutores, o Problema de Hopf e o estudo da estabilidade, vamos traçar relações entre a curvatura média de uma hipersuperfície e suas primas, as curvaturas de ordens mais altas.
x
Funções Harmônicas para Operadores Positivos e suas Aplicações em Dinâmica e Probabilidade
Horário:
21 de maio de 2021, das 9h às 10h.Link de transmissão:
https://youtu.be/lS5evR6NbO8Professor:
Leandro Cioletti (UnB)
Resumo:
Neste seminário vamos introduzir o espaço de funções harmônicas para operadores positivos e mostrar como a dimensão deste espaço está relacionada a um problema clássico em Física-Matemática de transição de fase.Vamos mostrar como esta nova teoria pode ser usada para construir um modelo probabilístico capaz de prever transições de fase da matéria entre três estados físicos. A construção concreta de tal modelo é hoje em dia um dos principais problemas em aberto em Física-Matemática e esta é a principal motivação do estudo a ser apresentado. As técnicas e os resultados são composto bela costura entre resultados clássicos de Análise, Teoria Ergódica, Sistemas Dinâmicos Hiperbólicos, Probabilidade e Mecânica Estatística. O objetivo é varrer todas as tecnicalidades envolvidas para baixo do tapete e ajudar o público a entender bem os progressos obtidos neste importante problema e mostrar alguns portas que nossos métodos abremna busca da solução deste problema.
x
Derivação, Análise e Aplicação em Transporte de Partículas
Horário:
18 de maio de 2021, das 9h às 10h.Link de transmissão:
https://youtu.be/pGQQ9iFpnmYProfessor:
Liliane Barichello (UFRGS)Resumo:
A teoria cinética dos gases tem sido, ao longo dos anos, foco de relevante pesquisa matemática. A Equação de Boltzmann, modelo matemático fundamental nesta área, desperta atenção por sua aplicação em muitas áreas e a sua desafiadora complexidade. A despeito da complexidade, intenso trabalho tem permitido avanços científicos e tecnológicos nos vários campos da ciência que se utilizam de simulações computacionais deste modelo. Nesta conferência, discutimos a construção dos chamados núcleos sintéticos de colisão, a partir da Equação Linearizada de Boltzmann, que determinam modelos matemáticos amplamente utilizados em simulações computacionais, particularmente em estudos no campo da nanotecnologia. Derivamos soluções de equações integrais originadas neste processo. Introduzimos, ainda, as condições de contorno de Cercignani-Lampis. Analisamos também esquemas numéricos envolvendo integração na esfera unitária, estes de interesse em aplicações médicas, como a tomografia ótica.
x
Um passeio sobre a geometria das superfícies em R³
Horário:
17 de maio de 2021, das 11h às 12h.Link de transmissão:
https://youtu.be/d8eBLSaZBygProfessor:
Marcos Petrúcio Cavalcante (UFAL)
Resumo:
Podemos considerar que a Geometria Diferencial nasceu com os trabalhos pioneiros de C. F. Gauss sobre o estudo das superfícies em R³. Desde então essa importante área da matemática se desenvolveu em muitas direções e também serviu de base para muitas pesquisas, inclusive para a Teoria da Relatividade Geral. Contudo, o estudo das superfícies em R³ ainda continua servindo de berço para muitos teoremas e também guarda em si a beleza que a visualização nos proporciona. Nesta palestra vamos apresentar alguns resultados importantes dessa teoria, com destaque para as superfícies mínimas e de curvatura média constante.
x
A construção de Kantor-Koecher-Tits: aplicação de representações de álgebras e superálgebras de Jordan
Horário:
20 de maio de 2021, das 10h às 11h.Link de transmissão:
https://youtu.be/rq3nuhQMtmUProfessor:
Iryna Kashuba (USP, SP)
Resumo:
Vamos revisar os resultados recentes sobre a determinação do tipo de representação de álgebras de Jordan de dimensão finita. A nossa principal ferramenta é a famosa construção Kantor-Koecher-Tits que fornece uma ponte entre a teoria de Jordan e a teoria de Lie. Se o tempo permitir, também falaremos sobre o uso da mesma abordagem para descrever representações indecomponíveis para superálgebras de Jordan simples que não são completamente redutíveis. É um trabalho conjunto com V. Serganova.
x
De sistemas de partículas a equações diferenciais parciais
Horário:
19 de maio de 2021, das 10h às 11h.Link de transmissão:
https://youtu.be/uQFVOD-nPlIProfessor:
Adriana Neumann (UFRGS)
Resumo:
Nesta palestra vamos mostrar como a obtenção de modelos macroscópicos, caracterizados por equações diferenciais parciais parabólicas, pode ser feita através de modelos microscópicos descritos por sistemas de partículas interagentes. Os sistemas de partículas interagentes que vamos apresentar possuem dinâmica descrita pelo processo de exclusão ou pelo modelo em meios porosos com alguma taxa lenta, que vai gerar condições de fronteira no modelo macroscópico associado.
x
A equação de Schrödinger: interação dos termos linear e não linear
Horário:
17 de maio de 2021, das 10h às 11h.Link de transmissão:
https://youtu.be/F6AgeB9LRkgProfessor:
Liliane de Almeida Maia (UnB)
Resumo:
Pretendemos revisitar resultados recentes de pesquisa sobre a equação de Schrödinger nas questões de existência, não existência e multiplicidade de soluções, procurando destacar o papel da interação entre um potencial, que multiplica um termo linear, e um termo não linear geral. Exploramos simetrias e teoria espectral.
x
Efeitos reais da política de taxa de juros e de compras de ativos arriscados pelo banco central
Horário:
19 de maio de 2021, das 9h às 10h.Local:
https://youtu.be/CSMUUtkKidwProfessor:
Susan Schommer (UFRJ)
Resumo:
Consideramos os efeitos da política monetária - taxas de juros nominais de curto prazo e compras de ativos arriscados pelo banco central - em um modelo de equilíbrio geral com precificação de ativos, restrições de colateral endógenas e preços rígidos. Mostramos que a escolha da política de taxas de juros que maximize o bem-estar é diferente dependendo do estado da economia e das restrições de colateral. Na ilustração numérica, mostramos que em um estado "ruim" da economia (em que as restrições de colateral estão ativas), a taxa de juros nominal ótima é zero e as compras de ativos arriscados pelo banco central podem levar a melhorias de Pareto dependendo especificamente do forma na qual os agentes estão restritos. Em um "bom" estado da economia, a taxa de juros ótima é positiva, e se as garantias (colateral) não estiverem ativas, as compras de ativos do banco central não afetam os preços ou as alocações de recursos na economia. Esse artigo é em conjunto com Aloisio Araujo (IMPA e EPGE-FGV) e Michael Woodford (Columbia University).
x
Mergulhos simpléticos e teoria dos números
Horário:
19 de maio de 2021, das 11h às 12h.Link de transmissão:
https://youtu.be/PtzadmWJMxsProfessor:
Vinicius Ramos (IMPA)
Resumo:
Uma das questões centrais em geometria simplética é o estudo dos mergulhos simpléticos. Nessa palestra, eu falarei sobre a história desse problema que se origina na mecânica clássica e como a sequência de Fibonacci aparece de uma forma surpreendente.
x
Sessão de Álgebra
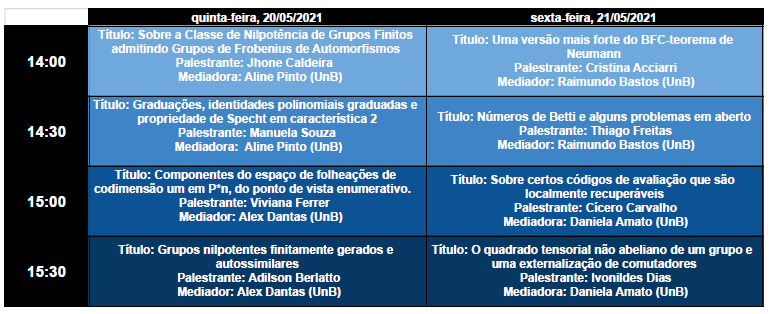
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/83585211059?pwd=Ynpld3JkWjUrZzB3QTM2dTk2K1piUT09
ID da reunião: 835 8521 1059
Senha de acesso: 057099
Coordenadores:
Aline Pinto (UnB)
Raimundo Bastos (UnB)
20 de maio de 2021
Jhone Caldeira (UFG), das 14:00 às 14:25
Título: Sobre a Classe de Nilpotência de Grupos Finitos
admitindo Grupos de Frobenius de Automorfismos.
Mediadora:Aline Pinto (UnB)
Resumo:
Manuela Souza (UFBA), das 14:30 às 14:55
Título: Graduações, identidades polinomiais graduadas e
propriedade de Specht em característica 2.
Mediadora: Aline Pinto (UnB)
Resumo:
Viviana Ferrer (UFF), das 15:00 às 15:25
Título: Componentes do espaço de folheações de
codimensão um em P*n, do ponto de vista enumerativo.
Mediador: Alex Dantas (UnB)
Resumo:
Adilson Berlatto (UFMT), das 15:30 às 15:55
Título: Grupos nilpotentes finitamente gerados e
autossimilares.
Mediador: Alex Dantas (UnB)
Resumo:
21 de maio de 2021
Cristina Acciarri (UnB), das 14:00 às 14:25
Título: Uma versão mais forte do BFC-teorema de Neumann.
Mediador: Raimundo Bastos (UnB)
Resumo:
Thiago Freitas (UTFPR), das 14:30 às 14:55
Título: Números de Betti e alguns problemas em aberto.
Mediador: Raimundo Bastos (UnB)
Resumo:
Cícero Carvalho (UFU), das 15:00 às 15:25
Título: Sobre certos códigos de avaliação que são
localmente recuperáveis.
MediadorA: Daniela Amato (UnB)
Resumo:
Ivonildes Dias (UFG), das 15:30 às 15:55
Título: O quadrado tensorial não abeliano de um grupo e
uma externalização de comutadores.
Mediadora: Daniela Amato (UnB)
Resumo:
Programação da sessão por dia
Mediadora:Aline Pinto (UnB)
Resumo:
Mediadora: Aline Pinto (UnB)
Resumo:
Mediador: Alex Dantas (UnB)
Resumo:
Mediador: Alex Dantas (UnB)
Resumo:
Mediador: Raimundo Bastos (UnB)
Resumo:
Mediador: Raimundo Bastos (UnB)
Resumo:
MediadorA: Daniela Amato (UnB)
Resumo:
Mediadora: Daniela Amato (UnB)
Resumo:
x
Sessão de Análise
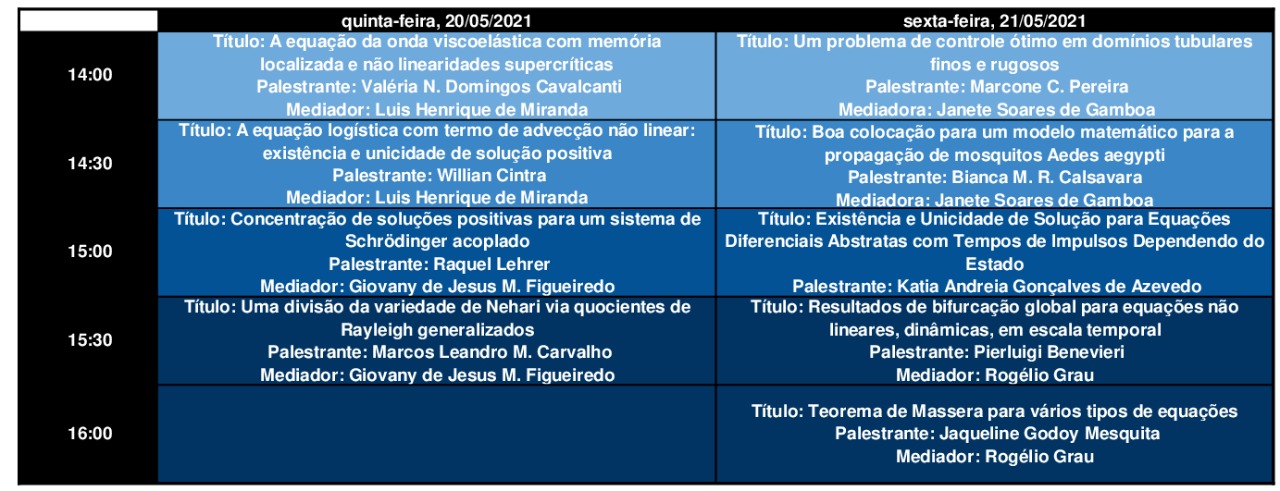
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/83845248907?pwd=d3FYL1ZRa09hQzN6T2UwMUx2Y3h5Zz09
ID da reunião: 838 4524 8907
Senha de acesso: 332896
Coordenadores:
Manuela Rezende (UnB)
Simone Bruschi (UnB)
20 de maio de 2021
Valéria N. Domingos Cavalcanti (UEM), das 14:00 às 14:30
Título: A equação da onda viscoelástica com memória
localizada e não linearidades supercríticas.
Mediador: Luis Henrique de Miranda
Resumo:
Willian Cintra (UNB), das 14:30 às 15:00
Título: A equação logística com termo de advecção não
linear: existência e unicidade de solução positiva.
Mediador: Luis Henrique de Miranda
Resumo:
Raquel Lehrer (Unioest), das 15:00 às 15:30
Título: Concentração de soluções positivas para um sistema de Schrödinger acoplado.
Mediador: Giovany de Jesus M. Figueiredo
Resumo:
Marcos Leandro M. Carvalho (IME-UFG), das 15:30 às 16:00
Título: Uma divisão da variedade de Nehari via quocientes de Rayleigh generalizados.
Mediador: Giovany de Jesus M. Figueiredo
Resumo:
21 de maio de 2021
Marcone C. Pereira (IME-USP) das 14:00 às 14:30
Título: Um problema de controle ótimo em domínios tubulares finos e rugosos.
Mediadora: Janete Soares de Gamboa
Resumo:
Bianca M. R. Calsavara (UNICAMP), das 14:30 às 15:00
Título: Boa colocação para um modelo matemático para a propagação de mosquitos Aedes aegypti.
Mediadora: Janete Soares de Gamboa
Resumo:
Katia Andreia Gonçalves de Azevedo (FFCLRP-USP), das 15:00 às 15:30
Título: Existência e Unicidade de Solução para Equações Diferenciais Abstratas com Tempos de Impulsos Dependendo do Estado.
Mediador: Rogélio Grau
Resumo:
Pierluigi Benevieri (IME-USP), das 15:30 às 16:00
Título: Resultados de bifurcação global para equações não lineares, dinâmicas, em escala temporal.
Mediador: Rogélio Grau
Resumo:
Jaqueline Godoy Mesquita (UnB), das 16:00 às 16:30
Título: Teorema de Massera para vários tipos de equações
Mediador: Rogélio Grau
Resumo:
Programação da sessão por dia
Mediador: Luis Henrique de Miranda
Resumo:
Mediador: Luis Henrique de Miranda
Resumo:
Mediador: Giovany de Jesus M. Figueiredo
Resumo:
Mediador: Giovany de Jesus M. Figueiredo
Resumo:
Mediadora: Janete Soares de Gamboa
Resumo:
Mediadora: Janete Soares de Gamboa
Resumo:
Mediador: Rogélio Grau
Resumo:
Mediador: Rogélio Grau
Resumo:
Mediador: Rogélio Grau
Resumo:
x
Sessão de Educação Matemática
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/83018349371?pwd=NTBvbXNtMC9QK0luelVIWTVKaTliUT09
ID da reunião: 830 1834 9371
Senha de acesso: 671728
Coordenadores:
Cleyton Gontijo (UnB)
Regina da Silva Pina Neves (UnB)
20 de maio de 2021
Marilena Bittar (UFMS), das 14:00 às 14:30
Título: A Educação Matemática como campo de atuação
profissional e de pesquisa na graduação na pósgraduação
Mediadora: Regina da Silva Pina Neves (UnB)
Wellington Lima Cedro (UFG), das 14:30 às 15:00
Título: A Educação Matemática como campo de atuação
profissional e de pesquisa na graduação na pósgraduação
Mediadora: Regina da Silva Pina Neves (UnB)
Resumo:
Marcelo de Carvalho Borba (UNESP), das 15:30 às 15:30
Título: A Educação Matemática como campo de atuação
profissional e de pesquisa na graduação na pósgraduação
Mediadora: Regina da Silva Pina Neves (UnB)
Resumo:
Debate, das 15:30 às 16:00
Título: A Educação Matemática como campo de atuação
profissional e de pesquisa na graduação na pósgraduação
Mediadora: Regina da Silva Pina Neves (UnB)
21 de maio de 2021
João Ricardo Viola dos Santos (UFMS), das 14:00 às 14:30
Título: Contribuições da Educação Matemática para a
avaliação da aprendizagem em matemática na educação
superior
Mediador: Cleyton Hércules Gontijo (UnB).
Guy Grebot (UnB), das 14:30 às 15:00
Título: Contribuições da Educação Matemática para a
avaliação da aprendizagem em matemática na educação
superior
Mediador: Cleyton Hércules Gontijo (UnB).
Resumo:
Wescley Well Vicente Bezerra (UnB), das 15:00 às 15:30
Título: Contribuições da Educação Matemática para a
avaliação da aprendizagem em matemática na educação
superior
Mediador:Cleyton Hércules Gontijo (UnB)
Resumo:
Debate, das 15:30 às 16:00
Título: A Educação Matemática como campo de atuação
profissional e de pesquisa na graduação na pósgraduação
Mediador: Cleyton Hércules Gontijo (UnB)
Programação da sessão por dia
Mediadora: Regina da Silva Pina Neves (UnB)
Mediadora: Regina da Silva Pina Neves (UnB)
Resumo:
Mediadora: Regina da Silva Pina Neves (UnB)
Resumo:
Mediadora: Regina da Silva Pina Neves (UnB)
Mediador: Cleyton Hércules Gontijo (UnB).
Mediador: Cleyton Hércules Gontijo (UnB).
Resumo:
Mediador:Cleyton Hércules Gontijo (UnB)
Resumo:
Mediador: Cleyton Hércules Gontijo (UnB)
x
Sessão de Geometria
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/84290754132?pwd=Q2Ixdk5CNzI0cEFDRndnNDNlSTBhQT09
ID da reunião: 842 9075 4132
Senha de acesso: 458024
Coordenadores:
João Paulo dos Santos (UnB)
José Luis Teruel (UnB)
20 de maio de 2021
Tarcísio Castro (UnB), das 14:00 às 14:30
Título: A note on isometric immersions and differential
equations which describe pseudospherical surfaces.
Mediador: José Luis Teruel Carretero
Resumo:
Miriam Telichevesky (UFRGS), das 14:35 às 15:05
Título: Problemas assintóticos em variedades de Hadamard
Mediador: José Luis Teruel Carretero
Resumo:
Benedito Leandro (UFG), das 15:10 às 15:40
Título: Mean-stable surfaces in Static Einstein-Maxwell theory
Mediador: João Paulo dos Santos
Resumo:
Valter Borges (UFPA), das 15:45 às 16:15
Título: Rigidity of Bach-flat Schouten Solitons
Mediador: João Paulo dos Santos
Resumo:
21 de maio de 2021
Hiuri Reis (IFG), das 14:00 às 14:30
Título:Sólitons do Fluxo Redutor de Curvas na Esfera.
Mediador: João Paulo dos Santos
Resumo:
Leandro Pessoa (UFPI), das 14:35 às 15:05
Título: Stochastic half-space theorems for minimal surfaces and H-surfaces of R³
Mediador: José Luis Teruel Carretero
Resumo:
Maria Andrade (UFS), das 15:10 às 15:40
Título: Resultados de classicação para superfícies CMC de bordo livre.
Mediador: José Luis Teruel Carretero
Resumo:
Hudson Pina (UFMT), das 15:45 às 16:15
Título:Rigidity of complete minimal submanifolds in a Hyperbolic space.
Mediador: João Paulo dos Santos
Resumo:
Programação da sessão por dia
Mediador: José Luis Teruel Carretero
Resumo:
Mediador: José Luis Teruel Carretero
Resumo:
Mediador: João Paulo dos Santos
Resumo:
Mediador: João Paulo dos Santos
Resumo:
Mediador: João Paulo dos Santos
Resumo:
Mediador: José Luis Teruel Carretero
Resumo:
Mediador: José Luis Teruel Carretero
Resumo:
Mediador: João Paulo dos Santos
Resumo:
x
Sessão de Matemática Aplicada

Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/83816434427?pwd=QUlYcjFPQW5Xa08wbWdqODJTTm5uZz09
ID da reunião: 838 1643 4427
Senha de acesso: 224141
Coordenadores:
Daniel Ventura (UFG)
Daniele Nantes (UnB)
20 de maio de 2021
Bruno Lopes (UFF), das 14:00 às 14:50
Título: Raciocinando sobre sistemas concorrentes com Reo.
Mediadora: Daniele Nantes (UnB).
Resumo:
Washington Ribeiro (IBICT), das 15:00 às 15:50
Título: Ciência Aberta, Publicações e Dados Científicos.
Mediadora: Daniele Nantes (UnB).
Resumo:
21 de maio de 2021
Julliano Rosa Nascimento (UFG), das 14:00 às 14:50
Título: Alguns Parâmetros de Convexidade para Prismas Complementares.
Mediador: Daniel Ventura (UnB).
Resumo:
Thaynara Arielly de Lima (UFG), das 15:00 às 15:50
Título: Formalizações matemática via assistentes de provas.
Mediador: Daniel Ventura (UnB).
Resumo:
Programação da sessão por dia
Mediadora: Daniele Nantes (UnB).
Resumo:
Mediadora: Daniele Nantes (UnB).
Resumo:
Mediador: Daniel Ventura (UnB).
Resumo:
Mediador: Daniel Ventura (UnB).
Resumo:
x
Sessão de Matemática e Covid-19
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/89553705264?pwd=djVXSk5NTUhkei9wR0M3VjlNZ0lQUT09
ID da reunião: 895 5370 5264
Senha de acesso: 359832
Coordenadores:
Dayse Pastore (CEFET/Rio)
Ma To Fu (UnB)
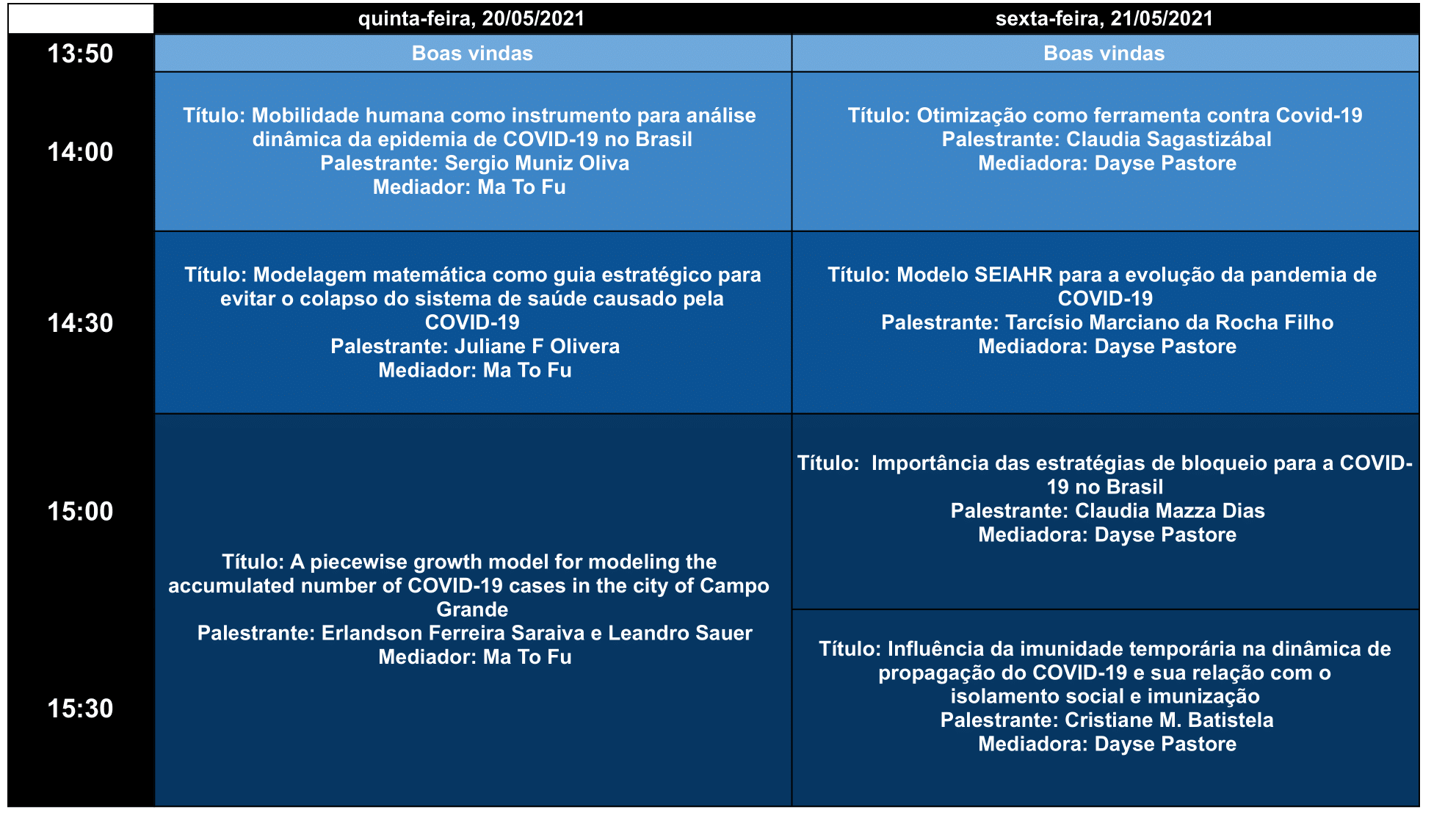
20 de maio de 2021
Sergio Muniz Oliva (USP), das 14:00 às 14:30
Título:: Mobilidade humana como instrumento para análise dinâmica da epidemia de COVID-19 no Brasil.
Mediador: Ma To Fu.
Resumo:
Juliane F Olivera (Fiocruz-BA), das 14:00 às 14:30
Título: Modelagem matemática como guia estratégico para evitar o colapso do sistema de saúde causado pela COVID-19.
Mediador: Ma To Fu.
Resumo:
Erlandson Ferreira Saraiva (UFMS) e Leandro Sauer (UFMS), das 14:00 às 15:00
Título: A piecewise growth model for modeling the accumulated number of COVID-19 cases in the city of Campo Grande.
Mediador: Ma To Fu.
Resumo:
21 de maio de 2021
Claudia Sagastizábal (Unicamp), das 14:00 às 14:30
Título: Otimização como ferramenta contra Covid-19.
Mediadora: Dayse Pastore.
Resumo:
Tarcísio Marciano da Rocha Filho (UnB), das 14:30 às 15:00
Título: Modelo SEIAHR para a evolução da pandemia de COVID-19.
Mediadora: Dayse Pastore.
Resumo:
Claudia Mazza Dias (UFRRJ), das 15:00 às 15:30
Título: Importância das estratégias de bloqueio para a COVID-19 no Brasil.
Mediadora: Dayse Pastore.
Resumo:
Cristiane M. Batistela (USP), das 15:30 às 16:00
Título: Influência da imunidade temporária na dinâmica de propagação do COVID-19 e sua relação com o isolamento social e imunização.
Mediadora: Dayse Pastore.
Resumo:
Programação da sessão por dia
Mediador: Ma To Fu.
Resumo:
Mediador: Ma To Fu.
Resumo:
Mediador: Ma To Fu.
Resumo:
Mediadora: Dayse Pastore.
Resumo:
Mediadora: Dayse Pastore.
Resumo:
Mediadora: Dayse Pastore.
Resumo:
Mediadora: Dayse Pastore.
Resumo:
x
Sessão de Probabilidade e Sistemas Dinâmicos
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/82999174259?pwd=V1U1L2V0UzFoY2w1aTlzS21uWDlYZz09
ID da reunião: 829 9917 4259
Senha de acesso: 626260
Coordenadores:
Mauro Patrão (UnB)
Paulo Henrique da Costa (UnB)
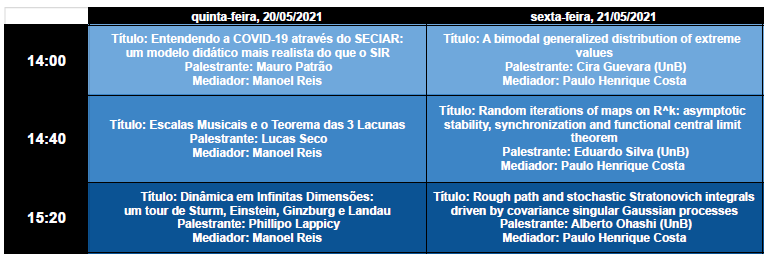
20 de maio de 2021
Mauro Patrão (UnB), das 14:00 às 14:40
Título: Entendendo a COVID-19 através do SECIAR: um modelo didático mais realista do que o SIR.
Mediador: Manoel Reis (UnB).
Resumo:
Lucas Seco (UnB), das 14:40 às 15:20
Título: Escalas Musicais e o Teorema das 3 Lacunas.
Mediador: Manoel Reis (UnB).
Resumo:
Phillipo Lappicy (ICMC), das 15:20 às 16:00
Título: Dinâmica em Infinitas Dimensões: um tour de Sturm, Einstein, Ginzburg e Landau.
Mediador: Manoel Reis (UnB).
Resumo:
21 de maio de 2021
Cira Guevara (UnB), das 14:00 às 14:40
Título: A bimodal generalized distribution of extreme values.
Mediador: Paulo Henrique Costa (UnB).
Resumo:
Eduardo Silva (UnB), das 14:40 às 15:20
Título: "Random iterations of maps on ℝk: asymptotic stability, synchronization and functional central limit theorem".
Mediador: Paulo Henrique Costa (UnB).
Resumo:
Alberto Ohashi (UnB), das 15:20 às 16:00
Título: Rough path and stochastic Stratonovich integrals driven by covariance singular Gaussian processes.
Mediador: Paulo Henrique Costa (UnB).
Resumo:
Programação da sessão por dia
Mediador: Manoel Reis (UnB).
Resumo:
Mediador: Manoel Reis (UnB).
Resumo:
Mediador: Manoel Reis (UnB).
Resumo:
Mediador: Paulo Henrique Costa (UnB).
Resumo:
Mediador: Paulo Henrique Costa (UnB).
Resumo:
Mediador: Paulo Henrique Costa (UnB).
Resumo:
x
Sessão de Teoria dos Números
Programação da sessão por dia
Link do Zoom:
https://us02web.zoom.us/j/82370772062?pwd=Y2F2UDBpVWxsTENVV0dnVmdlSElEUT09
ID da reunião: 823 7077 2062
Senha de acesso: 863528
Coordenadores:
Daiane Soares Veras (IFG)
Vinicius Facó (IFB)
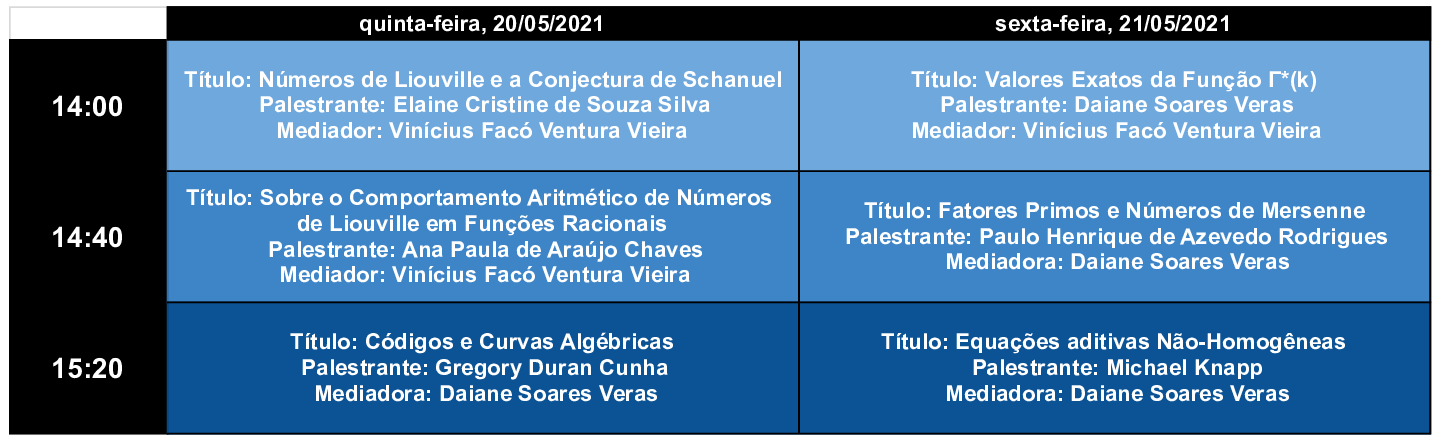
20 de maio de 2021
Elaine Cristine de Souza Silva (UFAL), das 14:00 às 14:40
Título: Números de Liouville e a Conjectura de Schanuel.
Mediador: Vinícius Facó Ventura Vieira (IFB).
Resumo:
Ana Paula de Araújo Chaves (UFG), das 14:40 às 15:20
Título: Sobre o Comportamento Aritmético de Números de Liouville em Funções Racionais.
Mediador: Vinícius Facó Ventura Vieira (IFB).
Resumo:
Gregory Duran Cunha (UFG), das 15:20 às 16:00
Título: Códigos e Curvas Algébricas.
Mediador: Daiane Soares Veras (IFG).
Resumo:
21 de maio de 2021
Daiane Soares Veras (IFG), das 14:00 às 14:40
Título: Valores Exatos da Função Γ*(k).
Mediador: Vinícius Facó Ventura Vieira (IFB).
Resumo:
Paulo Henrique de Azevedo Rodrigues (UFG), das 14:40 às 15:20
Título: Fatores Primos e Números de Mersenne.
Mediador: Daiane Soares Veras (IFG).
Resumo:
Michael Knapp (Loyola University Maryland), das 15:20 às 16:00
Título: Equações aditivas Não-Homogêneas.
Mediador: Daiane Soares Veras (IFG).
Resumo:
Programação da sessão por dia
Mediador: Vinícius Facó Ventura Vieira (IFB).
Resumo:
Mediador: Vinícius Facó Ventura Vieira (IFB).
Resumo:
Mediador: Daiane Soares Veras (IFG).
Resumo:
Mediador: Vinícius Facó Ventura Vieira (IFB).
Resumo:
Mediador: Daiane Soares Veras (IFG).
Resumo:
Mediador: Daiane Soares Veras (IFG).
Resumo:
x
Apresentação Musical, Samba
Horário:
19 de maio de 2021, das 20h às 21h.Link do Zoom:
https://us02web.zoom.us/j/83800423776?pwd=ZkNGakRrY3NYNmZHNTJQd3ZMeElSdz09ID da reunião: 838 0042 3776
Senha de acesso: 806097
Local:
Plataforma Zoom.Apresentadora:
Carol Nogueira
x
Apresentação Musical, Samba e Forró
Horário:
21 de maio de 2021, das 19h30 às 20h.Link do Zoom:
https://us02web.zoom.us/j/84956826978?pwd=T2R4eEhOTTR2N3F6SERLcWY2Vlc0dz09ID da reunião: 849 5682 6978
Senha de acesso: 267192
Local:
Plataforma Zoom.Apresentadora:
Carol Nogueira
x
Série "A Ciência como ela é" e Bate Papo com Marcia Barbosa e Carolina Brito
Horários:
Breve Introdução à série "A Ciência como ela é": 20 de maio de 2021, das 18h30 às 19h.Série "A Ciência como ela é": 20 de maio de 2021, das 19h às 20h.
Bate Papo com Marcia Barbosa e Carolina Brito: 20 de maio de 2021, das 20h às 21h.
Links da transmissão:
Breve Introdução à série "A Ciência como ela é": https://youtu.be/nCGurGRor8USérie "A Ciência como ela é": https://youtu.be/Lphqe1f7gt0
Bate Papo com Marcia Barbosa e Carolina Brito: https://youtu.be/OMm-R11Oo6w
Mediadoras:
Susanne Maciel (UnB)
Dayse Haime Pastore (CEFET/RJ)

Convidadas:
Carolina Brito (UFRGS)
Marcia Barbosa (UFRGS)
